Skip to content
Rational and Radical Functions: Get Stronger Answer Key
Rational Functions
- All reals [latex]x \neq 1[/latex], [latex]1[/latex]
- All reals [latex]x \neq -1, -2, 1, 2[/latex]
- V.A. at [latex]x=-\dfrac{2}{5}[/latex]; H.A. at [latex]y=0[/latex]; Domain is all reals [latex]x \neq -\dfrac{2}{5}[/latex]
- V.A. at [latex]x=4, -9[/latex]; H.A. at [latex]y=0[/latex]; Domain is all reals [latex]x \neq 4, -9[/latex]
- V.A. at [latex]x=0, 4, -4[/latex]; H.A. at [latex]y=0[/latex]; Domain is all reals [latex]x \neq 0, 4, -4[/latex]
- V.A. at [latex]x=5[/latex]; H.A. at [latex]y=0[/latex]; Domain is all reals [latex]x \neq 5, -5[/latex]
- V.A. at [latex]x=\dfrac{1}{3}[/latex]; H.A. at [latex]y=-\dfrac{2}{3}[/latex]; Domain is all reals [latex]x \neq \dfrac{1}{3}[/latex]
- none
- [latex]x[/latex]-intercepts none, [latex]y[/latex]-intercept [latex](0, \dfrac{1}{4})[/latex]
- Local behavior: [latex]x \to -\dfrac{1}{2}^+[/latex], [latex]f(x) \to -\infty[/latex], [latex]x \to -\dfrac{1}{2}^-[/latex], [latex]f(x) \to \infty[/latex] End behavior: [latex]x \to \pm\infty[/latex], [latex]f(x) \to \dfrac{1}{2}[/latex]
- Local behavior: [latex]x \to 6^+[/latex], [latex]f(x) \to -\infty[/latex], [latex]x \to 6^-[/latex], [latex]f(x) \to \infty[/latex], End behavior: [latex]x \to \pm\infty[/latex], [latex]f(x) \to -2[/latex]
- Local behavior: [latex]x \to \dfrac{1}{3}^+[/latex], [latex]f(x) \to -\infty[/latex], [latex]x \to \dfrac{1}{3}^-[/latex], [latex]f(x) \to \infty[/latex], [latex]x \to \dfrac{5}{2}^+[/latex], [latex]f(x) \to \infty[/latex], [latex]x \to \dfrac{5}{2}^-[/latex], [latex]f(x) \to -\infty[/latex] End behavior: [latex]x \to \pm\infty[/latex], [latex]f(x) \to \dfrac{1}{3}[/latex]
- [latex]y = 2x + 4[/latex]
- [latex]y = -2x[/latex]
- V.A. [latex]x=-4[/latex], H.A. [latex]y=2[/latex]; [latex](\dfrac{3}{2},0)[/latex]; [latex](0,-\dfrac{3}{4})[/latex]
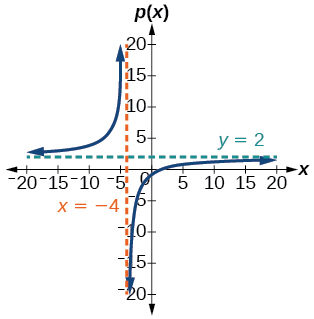
- V.A. [latex]x=2[/latex], H.A. [latex]y=0[/latex], [latex](0,1)[/latex]
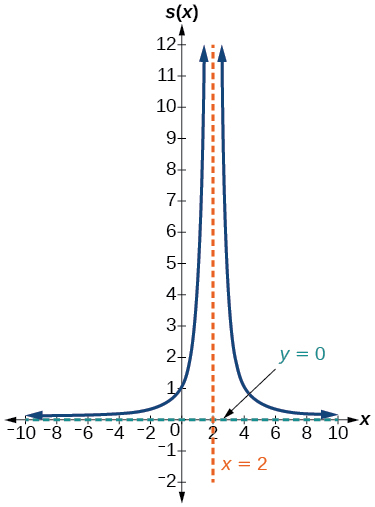
- V.A. [latex]x=-4[/latex], [latex]x=\dfrac{4}{3}[/latex], H.A. [latex]y=1[/latex]; [latex](5,0)[/latex]; [latex](-\dfrac{1}{3},0)[/latex]; [latex](0,\dfrac{5}{16})[/latex]
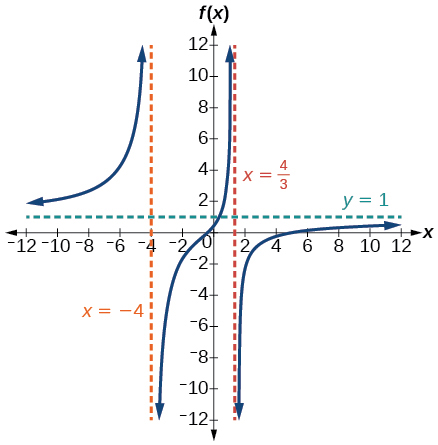
- V.A. [latex]x=-1[/latex], H.A. [latex]y=1[/latex]; [latex](-3,0)[/latex]; [latex](0,3)[/latex]
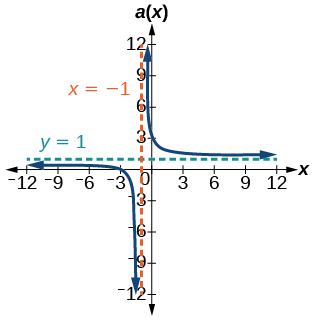
- [latex]y = 50\dfrac{x^2-x-2}{x^2-25}[/latex]
- [latex]y = 7\dfrac{x^2+2x-24}{x^2+9x+20}[/latex]
- [latex]y = \dfrac{1}{2}\dfrac{x^2-4x+4}{x+1}[/latex]
- [latex]y = 4\dfrac{x-3}{x^2-x-12}[/latex]
- [latex]y = \dfrac{27(x-2)}{(x+3)(x-3)^2}[/latex]
- [latex]C(t) = \dfrac{8+2t}{300+20t}[/latex]
- After about [latex]6.12[/latex] hours.
- [latex]A(x) = 50x^2 + \dfrac{800}{x}[/latex]. [latex]2[/latex] by [latex]2[/latex] by [latex]5[/latex] feet.
- [latex]A(x) = \pi x^2 + \dfrac{100}{x}[/latex]. Radius = [latex]2.52[/latex] meters.
Inverses and Radical Functions
- [latex]f^{-1}(x) = \sqrt{x + 4}[/latex]
- [latex]f^{-1}(x) = \sqrt{x + 3} - 1[/latex]
- [latex]f^{-1}(x) = \sqrt{12 - x}[/latex]
- [latex]f^{-1}(x) = \pm\sqrt{\dfrac{x-4}{2}}[/latex]
- [latex]f^{-1}(x) = \sqrt{\dfrac{x-1}{3}-3}[/latex]
- [latex]f^{-1}(x) = \sqrt{\dfrac{4-x}{2}-3}[/latex]
- [latex]f^{-1}(x) = \dfrac{3-x^2}{4}[/latex], [latex][0,\infty)[/latex]
- [latex]f^{-1}(x) = \dfrac{(x-5)^2+8}{6}[/latex]
- [latex]f^{-1}(x) = (3 - x)^2[/latex]
- [latex]f^{-1}(x) = \dfrac{4x+3}{7}[/latex]
- [latex]f^{-1}(x) = \dfrac{7x-3}{1-x}[/latex]
- [latex]f^{-1}(x) = \dfrac{2x-1}{5x+5}[/latex]
- [latex]f^{-1}(x) = \sqrt{x + 3} - 2[/latex]
- [latex]f^{-1}(x) = \sqrt{x - 2}[/latex]
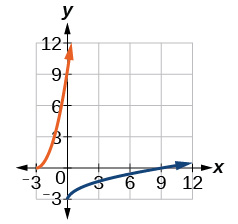
- [latex]f^{-1}(x) = \sqrt{x - 3}[/latex]
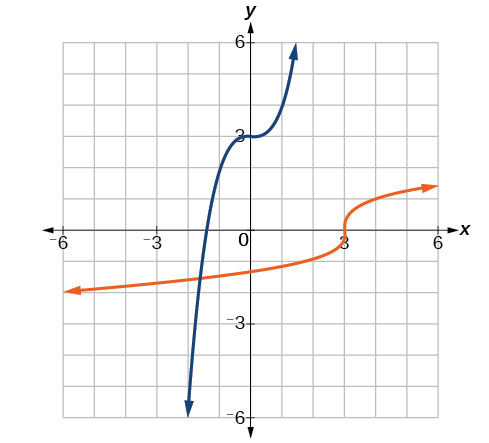
- [latex]f^{-1}(x) = \sqrt[3]{x - 3}[/latex]

- [latex][-1,0] \cup [1,\infty)[/latex]
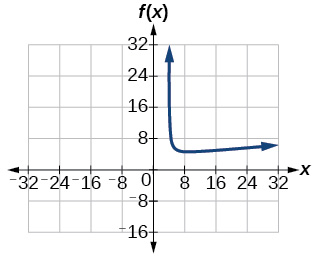
- [latex][-3,0] \cup (4,\infty)[/latex]
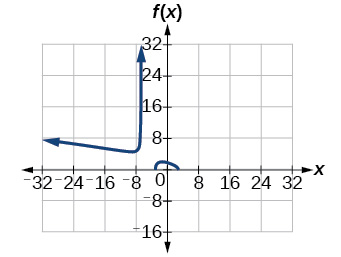
- [latex][-\infty,-4] \cdot [-3,3][/latex]
- [latex]t(h) = \sqrt{\dfrac{600-h}{16}}[/latex], [latex]3.54[/latex] seconds
- [latex]r(A) = \sqrt{\dfrac{A}{4\pi}}[/latex], [latex]\approx 8.92[/latex] in.
- [latex]l(T) = 32.2\left(\dfrac{T}{2\pi}\right)[/latex], [latex]\approx 3.26[/latex]ft
- [latex]r(A) = \sqrt{\dfrac{A+8\pi}{2\pi}}-2[/latex], [latex]3.99[/latex] ft
- [latex]r(V) = \sqrt{\dfrac{V}{10\pi}}[/latex], [latex]\approx 5.64[/latex] ft
Variations
- [latex]y = 5x^2[/latex]
- [latex]y = \dfrac{1}{1944}x^3[/latex]
- [latex]y = 6x^4[/latex]
- [latex]y = \dfrac{18}{x^2}[/latex]
- [latex]y = \dfrac{81}{x^4}[/latex]
- [latex]y = \dfrac{20}{\sqrt[3]{x}}[/latex]
- [latex]y = 10xzw[/latex]
- [latex]y = 10x\sqrt{z}[/latex]
- [latex]y = 4\dfrac{xz}{w}[/latex]
- [latex]y = 40\dfrac{xz}{\sqrt{wt^2}}[/latex]
- [latex]y = 256[/latex]
- [latex]y = 6[/latex]
- [latex]y = 6[/latex]
- [latex]y = 27[/latex]
- [latex]y = 3[/latex]
- [latex]y = 18[/latex]
- [latex]y = 90[/latex]
- [latex]y = \dfrac{81}{2}[/latex]
- [latex]3[/latex] seconds
- [latex]48[/latex] inches
- [latex]49.75[/latex] pounds
- [latex]33.33[/latex] amperes
- [latex]2.88[/latex] inches









