Polynomial Functions: Get Stronger Key
Quadratic Functions Solutions
3. If [latex]a=0[/latex] then the function becomes a linear function.
5. If possible, we can use factoring. Otherwise, we can use the quadratic formula.
7. [latex]f\left(x\right)={\left(x+1\right)}^{2}-2[/latex], Vertex [latex]\left(-1,-4\right)[/latex]
11. [latex]f\left(x\right)=3{\left(x - 1\right)}^{2}-12[/latex], Vertex [latex]\left(1,-12\right)[/latex]
15. Minimum is [latex]-\frac{17}{2}[/latex] and occurs at [latex]\frac{5}{2}[/latex]. Axis of symmetry is [latex]x=\frac{5}{2}[/latex].
17. Minimum is [latex]-\frac{17}{16}[/latex] and occurs at [latex]-\frac{1}{8}[/latex]. Axis of symmetry is [latex]x=-\frac{1}{8}[/latex].
21. Domain is [latex]\left(-\infty ,\infty \right)[/latex]. Range is [latex]\left[2,\infty \right)[/latex].
23. Domain is [latex]\left(-\infty ,\infty \right)[/latex]. Range is [latex]\left[-5,\infty \right)[/latex].
29. [latex]\left\{3i\sqrt{3},-3i\sqrt{3}\right\}[/latex]
31. [latex]\left\{2+i,2-i\right\}[/latex]
35. [latex]\left\{5+i,5-i\right\}[/latex]
39. [latex]\left\{-\frac{1}{2}+\frac{3}{2}i, -\frac{1}{2}-\frac{3}{2}i\right\}[/latex]
41. [latex]\left\{-\frac{3}{5}+\frac{1}{5}i, -\frac{3}{5}-\frac{1}{5}i\right\}[/latex]
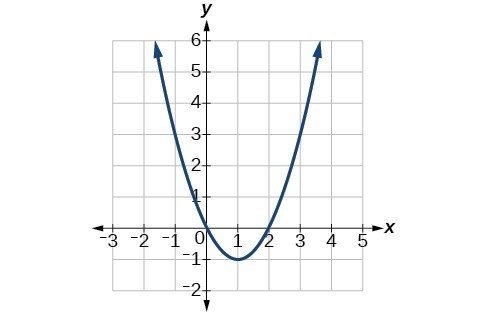
53. Vertex [latex]\left(1,\text{ }-1\right)[/latex], Axis of symmetry is [latex]x=1[/latex]. Intercepts are [latex]\left(0,0\right), \left(2,0\right)[/latex].
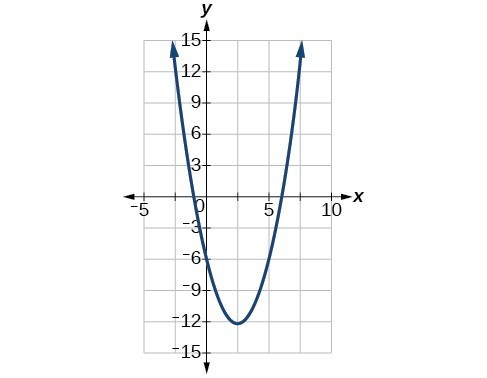
55. Vertex [latex]\left(\frac{5}{2},\frac{-49}{4}\right)[/latex], Axis of symmetry is [latex]\left(0,-6\right),\left(-1,0\right),\left(6,0\right)[/latex].
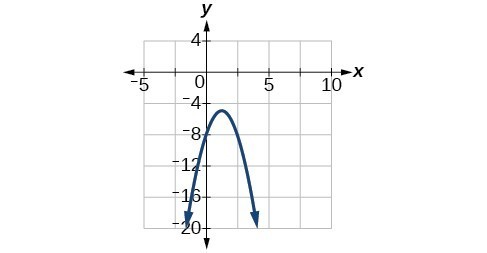
57. Vertex [latex]\left(\frac{5}{4}, -\frac{39}{8}\right)[/latex], Axis of symmetry is [latex]x=\frac{5}{4}[/latex]. Intercepts are [latex]\left(0, -8\right)[/latex].
59. [latex]f\left(x\right)={x}^{2}-4x+1[/latex]
61. [latex]f\left(x\right)=-2{x}^{2}+8x - 1[/latex]
63. [latex]f\left(x\right)=\frac{1}{2}{x}^{2}-3x+\frac{7}{2}[/latex]
65. [latex]f\left(x\right)={x}^{2}+1[/latex]
67. [latex]f\left(x\right)=2-{x}^{2}[/latex]
69. [latex]f\left(x\right)=2{x}^{2}[/latex]
85. 50 feet by 50 feet. Maximize [latex]f\left(x\right)=-{x}^{2}+100x[/latex].
91. 2909.56 meters
93. $10.70
Polynomial Functions Solutions
1. The coefficient of the power function is the real number that is multiplied by the variable raised to a power. The degree is the highest power appearing in the function.
3. As x decreases without bound, so does [latex]f\left(x\right)[/latex]. As x increases without bound, so does [latex]f\left(x\right)[/latex].
13. Degree = 2, Coefficient = –2
15. Degree =4, Coefficient = –2
17. [latex]\text{As }x\to \infty ,f\left(x\right)\to \infty ,\text{ as }x\to -\infty ,f\left(x\right)\to \infty[/latex]
21. [latex]\text{As }x\to -\infty ,f\left(x\right)\to -\infty ,\text{ as }x\to \infty ,f\left(x\right)\to -\infty[/latex]
23. [latex]\text{As }x\to \infty ,f\left(x\right)\to \infty ,\text{ as }x\to -\infty ,f\left(x\right)\to -\infty[/latex]
25. y-intercept is [latex]\left(0,12\right)[/latex], t-intercepts are [latex]\left(1,0\right);\left(-2,0\right);\text{and }\left(3,0\right)[/latex].
27. y-intercept is [latex]\left(0,-16\right)[/latex]. x-intercepts are [latex]\left(2,0\right)[/latex] and [latex]\left(-2,0\right)[/latex].
29. y-intercept is [latex]\left(0,0\right)[/latex].i x-intercepts are [latex]\left(0,0\right),\left(4,0\right)[/latex], and [latex]\left(-2, 0\right)[/latex].
31. 3
33. 5
47. [latex]\text{As }x\to -\infty ,f\left(x\right)\to \infty ,\text{ as }x\to \infty ,f\left(x\right)\to \infty[/latex]
| x | f(x) |
|---|---|
| 10 | 9,500 |
| 100 | 99,950,000 |
| –10 | 9,500 |
| –100 | 99,950,000 |
49. [latex]\text{As }x\to -\infty ,f\left(x\right)\to \infty ,\text{ as }x\to \infty ,f\left(x\right)\to -\infty[/latex]
| x | f(x) |
|---|---|
| 10 | –504 |
| 100 | –941,094 |
| –10 | 1,716 |
| –100 | 1,061,106 |
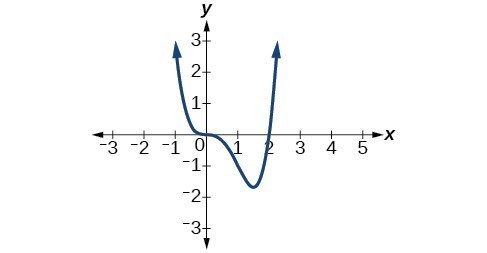
51. The y-intercept is [latex]\left(0, 0\right)[/latex]. The x-intercepts are [latex]\left(0, 0\right),\text{ }\left(2, 0\right)[/latex]. [latex]\text{As }x\to -\infty ,f\left(x\right)\to \infty ,\text{ as }x\to \infty ,f\left(x\right)\to \infty[/latex]
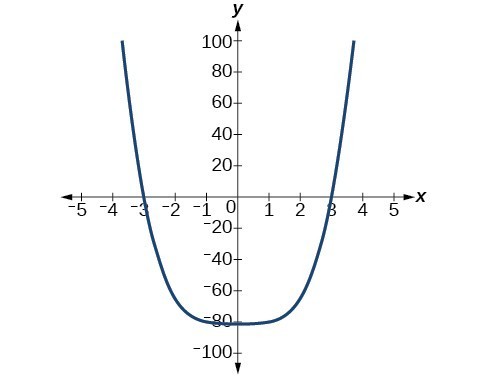
57. The y-intercept is [latex]\left(0, -81\right)[/latex]. The x-intercept are [latex]\left(3, 0\right),\text{ }\left(-3, 0\right)[/latex]. [latex]\text{As }x\to -\infty ,f\left(x\right)\to \infty ,\text{ as }x\to \infty ,f\left(x\right)\to \infty[/latex]
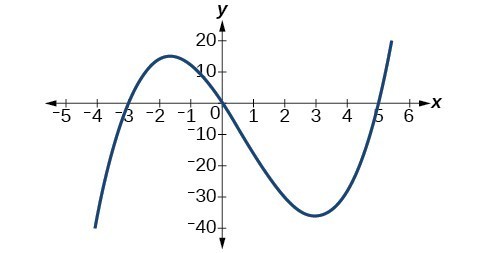
59. The y-intercept is [latex]\left(0, 0\right)[/latex]. The x-intercepts are [latex]\left(-3, 0\right),\text{ }\left(0, 0\right),\text{ }\left(5, 0\right)[/latex]. [latex]\text{As }x\to -\infty ,f\left(x\right)\to -\infty ,\text{ as }x\to \infty ,f\left(x\right)\to \infty[/latex]
61. [latex]f\left(x\right)={x}^{2}-4[/latex]
63. [latex]f\left(x\right)={x}^{3}-4{x}^{2}+4x[/latex]
65. [latex]f\left(x\right)={x}^{4}+1[/latex]
69. [latex]V\left(x\right)=4{x}^{3}-32{x}^{2}+64x[/latex]
Graphs of Polynomial Functions Solutions
1. The x-intercept is where the graph of the function crosses the x-axis, and the zero of the function is the input value for which [latex]f\left(x\right)=0[/latex].
7. [latex]\left(-2,0\right),\left(3,0\right),\left(-5,0\right)[/latex]
9. [latex]\left(3,0\right),\left(-1,0\right),\left(0,0\right)[/latex]
13. [latex]\left(0,0\right),\text{ }\left(-5,0\right),\text{ }\left(4,0\right)[/latex]
17. [latex]\left(-2,0\right),\left(2,0\right),\left(\frac{1}{2},0\right)[/latex]
19. [latex]\left(1,0\right),\text{ }\left(-1,0\right)[/latex]
21. [latex]\left(0,0\right),\left(\sqrt{3},0\right),\left(-\sqrt{3},0\right)[/latex]
25. [latex]f\left(2\right)=-10[/latex] and [latex]f\left(4\right)=28[/latex]. Sign change confirms.
27. [latex]f\left(1\right)=3[/latex] and [latex]f\left(3\right)=-77[/latex]. Sign change confirms.
31. 0 with multiplicity 2, [latex]-\frac{3}{2}[/latex] with multiplicity 5, 4 with multiplicity 2
33. 0 with multiplicity 2, –2 with multiplicity 2
37. [latex]\text{0}\text{ with multiplicity }4\text{,}2\text{ with multiplicity }1\text{,}-\text{1}\text{ with multiplicity }1[/latex]
39. [latex]\frac{3}{2}[/latex] with multiplicity 2, 0 with multiplicity 3
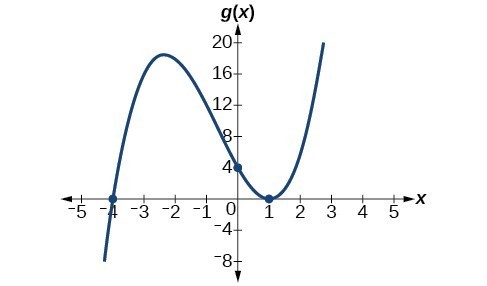
43. x-intercepts, [latex]\left(1, 0\right)[/latex] with multiplicity 2, [latex]\left(-4, 0\right)[/latex] with multiplicity 1, y-intercept [latex]\left(0, 4\right)[/latex]. As [latex]x\to -\infty[/latex] , [latex]f\left(x\right)\to -\infty[/latex] , as [latex]x\to \infty[/latex] , [latex]f\left(x\right)\to \infty[/latex] .
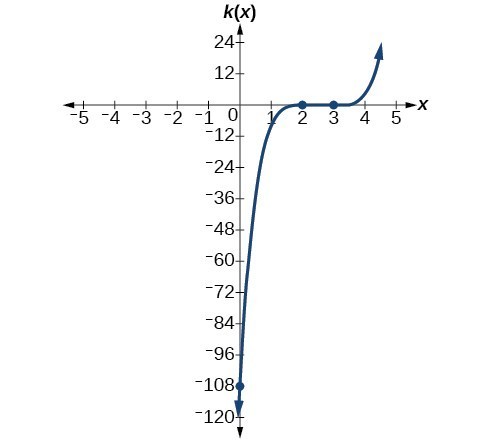
45. x-intercepts [latex]\left(3,0\right)[/latex] with multiplicity 3, [latex]\left(2,0\right)[/latex] with multiplicity 2, y-intercept [latex]\left(0,-108\right)[/latex] . As [latex]x\to -\infty[/latex], [latex]f\left(x\right)\to -\infty[/latex] , as [latex]x\to \infty[/latex] , [latex]f\left(x\right)\to \infty[/latex].
47. x-intercepts [latex]\left(0, 0\right),\left(-2, 0\right),\left(4, 0\right)[/latex] with multiplicity 1, y-intercept [latex]\left(0, 0\right)[/latex]. As [latex]x\to -\infty[/latex] , [latex]f\left(x\right)\to \infty[/latex] , as [latex]x\to \infty[/latex] , [latex]f\left(x\right)\to -\infty[/latex].
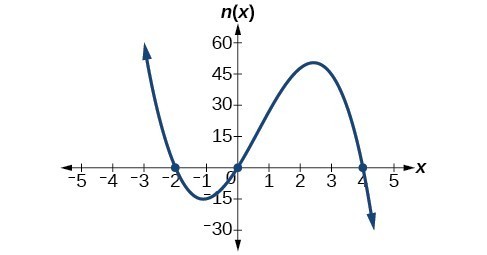
49. [latex]f\left(x\right)=-\frac{2}{9}\left(x - 3\right)\left(x+1\right)\left(x+3\right)[/latex]
53. [latex]f\left(x\right)=-\frac{1}{8}\left(x +4\right)\left(x+2\right)\left(x-1\right)\left(x-3\right)[/latex]
55. [latex]f\left(x\right)=\frac{1}{12}\left(x +2\right)^2\left(x+3\right)^2[/latex]
59. [latex]f\left(x\right)=\frac{1}{3}{\left(x - 3\right)}^{2}{\left(x - 1\right)}^{2}\left(x+3\right)[/latex]
63. [latex]f\left(x\right)=-2\left(x+3\right)\left(x+2\right)\left(x - 1\right)[/latex]
65. [latex]f\left(x\right)=-\frac{3}{2}{\left(2x - 1\right)}^{2}\left(x - 6\right)\left(x+2\right)[/latex]
75. [latex]f\left(x\right)=4{x}^{3}-36{x}^{2}+80x[/latex]
77. [latex]f\left(x\right)=4{x}^{3}-36{x}^{2}+60x+100[/latex]
79. [latex]f\left(x\right)=\pi \left(9{x}^{3}+45{x}^{2}+72x+36\right)[/latex]