Dividing Polynomials Solutions

1. The binomial is a factor of the polynomial.

3. [latex]x+6+\frac{5}{x - 1}\text{,}\text{quotient:}x+6\text{,}\text{remainder:}\text{5}[/latex]

7. [latex]x - 5\text{,}\text{quotient: }x - 5\text{,}\text{remainder: }\text{0}[/latex]

13. [latex]2{x}^{2}-3x+5\text{,}\text{quotient:}2{x}^{2}-3x+5\text{,}\text{remainder: }\text{0}[/latex]

15. [latex]2{x}^{2}+2x+1+\frac{10}{x - 4}[/latex]

19. [latex]3{x}^{2}-11x+34-\frac{106}{x+3}[/latex]

23. [latex]4{x}^{2}-21x+84-\frac{323}{x+4}[/latex]

29. [latex]{x}^{3}-3x+1[/latex]

43. [latex]\text{Quotient: }4{x}^{2}+8x+16\text{,}\text{remainder: }-1[/latex]

45. [latex]\text{Quotient: }3{x}^{2}+3x+5\text{,}\text{remainder: }0[/latex]

61. [latex]2x+3[/latex]

63. [latex]x+2[/latex]

Complex Numbers Solutions

1. Add the real parts together and the imaginary parts together.

3. i times i equals –1, which is not imaginary. (answers vary)

7. [latex]14+7i[/latex]

9. [latex]-\frac{23}{29}+\frac{15}{29}i[/latex]

13.

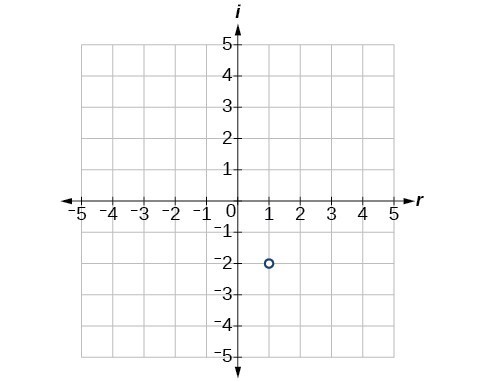
15.

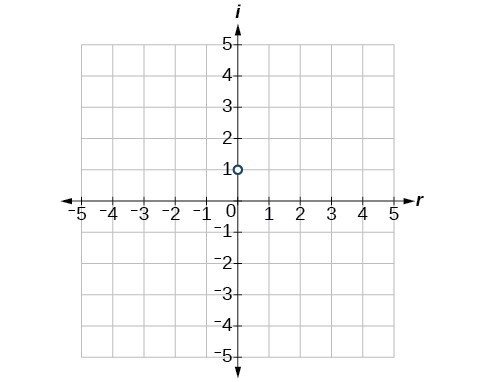
17. [latex]8-i[/latex]

19. [latex]-11+4i[/latex]

23. [latex]6+15i[/latex]

25. [latex]-16+32i[/latex]

27. [latex]-4 - 7i[/latex]

29. 25

33. [latex]4 - 6i[/latex]

35. [latex]\frac{2}{5}+\frac{11}{5}i[/latex]

37. 15i

39. [latex]1+i\sqrt{3}[/latex]

41. 1

43. –1

Zeros of Polynomial Functions Solutions

3. Rational zeros can be expressed as fractions whereas real zeros include irrational numbers.

5. Polynomial functions can have repeated zeros, so the fact that number is a zero doesn’t preclude it being a zero again.

7. –106

9. 0

11. 255

13. –1

15. –2, 1, [latex]\frac{1}{2}[/latex]

21. [latex]-\frac{5}{2}, \sqrt{6}, -\sqrt{6}[/latex]

23. [latex]2, -4, -\frac{3}{2}[/latex]

25. 4, –4, –5

29. [latex]\frac{1}{2}, \frac{1+\sqrt{5}}{2}, \frac{1-\sqrt{5}}{2}[/latex]

31. [latex]\frac{3}{2}[/latex]

33. 2, 3, –1, –2

37. [latex]-1, -1, \sqrt{5}, -\sqrt{5}[/latex]

41. [latex]2, 3+2i, 3 - 2i[/latex]

45. [latex]-\frac{1}{2}, 1+4i, 1 - 4i[/latex]

57. [latex]\pm 5, \pm 1, \pm \frac{5}{2}[/latex]

59. [latex]\pm 1, \pm \frac{1}{2}, \pm \frac{1}{3}, \pm \frac{1}{6}[/latex]

61. [latex]1, \frac{1}{2}, -\frac{1}{3}[/latex]

63. [latex]2, \frac{1}{4}, -\frac{3}{2}[/latex]

65. [latex]\frac{5}{4}[/latex]

71. 8 by 4 by 6 inches

75. 8 by 5 by 3 inches

Inverses and Radical Functions Solutions

1. It can be too difficult or impossible to solve for x in terms of y.

3. We will need a restriction on the domain of the answer.

5. [latex]{f}^{-1}\left(x\right)=\sqrt{x}+4[/latex]

7. [latex]{f}^{-1}\left(x\right)=\sqrt{x+3}-1[/latex]

9. [latex]{f}^{-1}\left(x\right)=-\sqrt{\frac{x - 5}{3}}[/latex]

11. [latex]f\left(x\right)=\sqrt{9-x}[/latex]

31. [latex]{f}^{-1}\left(x\right)=\sqrt{x+6}+3[/latex]

13. [latex]{f}^{-1}\left(x\right)=\sqrt[3]{x - 5}[/latex]

17. [latex]{f}^{-1}\left(x\right)=\frac{{x}^{2}-1}{2},\left[0,\infty \right)[/latex]

21. [latex]{f}^{-1}\left(x\right)={\left(\frac{x - 9}{2}\right)}^{3}[/latex]

23. [latex]{f}^{-1}\left(x\right)={\frac{2 - 8x}{x}}[/latex]

25. [latex]{f}^{-1}\left(x\right)=\frac{7x - 3}{1-x}[/latex]

35. [latex]{f}^{-1}\left(x\right)=\sqrt{x}+4[/latex]

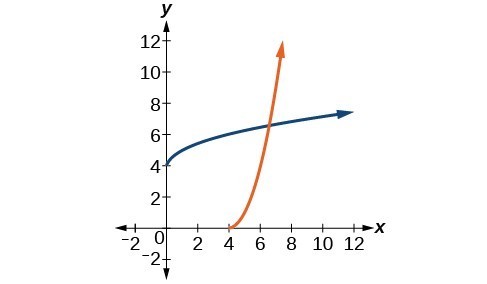
37. [latex]{f}^{-1}\left(x\right)=\sqrt[3]{1-x}[/latex]

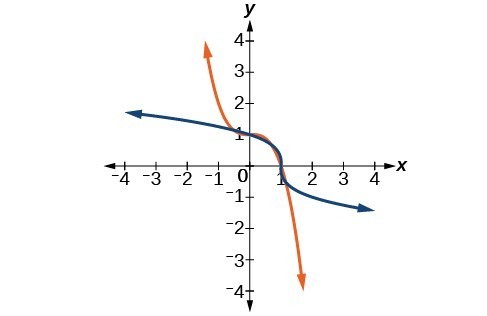
41. [latex]{f}^{-1}\left(x\right)=\sqrt{\frac{1}{x}}[/latex]

57. [latex]t\left(h\right)=\sqrt{\frac{200-h}{4.9}}[/latex], 5.53 seconds

59. [latex]r\left(V\right)=\sqrt[3]{\frac{3V}{4\pi }}[/latex], 3.63 feet