Exponential and Logarithmic Functions: Get Stronger Key
Exponential Functions
2. Yes. In an exponential function written as [latex]f(x)=ab^x[/latex], the base [latex]b[/latex] determines growth or decay: if [latex]b>1[/latex] the function grows; if [latex]0 5. Exponential function. “Decreases by a factor of [latex]\frac{1}{8}[/latex] every 24 hours” means each 24-hour period multiplies the population by a constant ratio [latex]\frac{1}{8}[/latex]. 6. Exponential function. Increasing by 3.25% annually means the value is multiplied each year by the constant factor [latex]1.0325[/latex]. 7. Not exponential. Subtracting $5 each session is a constant difference (linear), not a constant ratio. 9. Forest [latex]B[/latex] grows faster because its growth factor is larger: [latex]1.029>1.025[/latex]. 10. Forest [latex]A[/latex] had more trees initially: [latex]A(0)=115[/latex] and [latex]B(0)=82[/latex], so forest [latex]A[/latex] had [latex]115-82=33[/latex] more trees. 11. After 20 years: [latex]A(20)\approx 188[/latex] and [latex]B(20)\approx 145[/latex]. Forest [latex]A[/latex] will have about [latex]188-145=43[/latex] more trees. 12. After 100 years: [latex]A(100)\approx 1359[/latex] and [latex]B(100)\approx 1430[/latex]. Forest [latex]B[/latex] will have about [latex]1430-1359=71[/latex] more trees. 15. Exponential growth because the base is [latex]1.06>1[/latex]. 17. Exponential decay because the base is [latex]0.97[/latex] and [latex]0<0.97<1[/latex]. 19. Let [latex]f(x)=ab^x[/latex]. From [latex](0,2000)[/latex], [latex]a=2000[/latex]. Using [latex](2,20)[/latex]: [latex]20=2000b^2\Rightarrow b^2=0.01\Rightarrow b=0.1[/latex]. So [latex]f(x)=2000(0.1)^x[/latex]. 21. Let [latex]f(x)=ab^x[/latex]. Using [latex](-2,6)[/latex] and [latex](3,1)[/latex], the function is [latex]f(x)=6^{\frac{3}{5}}\left(6^{-\frac{1}{5}}\right)^x[/latex] (equivalently [latex]f(x)=6^{\frac{3-x}{5}}[/latex]). 23. Linear. The differences are constant: [latex]40-70=-30[/latex], [latex]10-40=-30[/latex], [latex]-20-10=-30[/latex]. 25. Neither. The differences are not constant and the ratios are not constant, so it is not linear or exponential. 31. [latex]A(t)=P\left(1+\frac{r}{n}\right)^{nt}[/latex] with [latex]P=6500[/latex], [latex]r=0.036[/latex], [latex]n=2[/latex], [latex]t=20[/latex]: [latex]A\approx 6500(1.018)^{40}\approx \$13{,}268.58[/latex]. 32. Weekly compounding: [latex]n=52[/latex]. [latex]A\approx 6500\left(1+\frac{0.036}{52}\right)^{52\cdot 20}\approx \$13{,}350.49[/latex]. This is about [latex]\$13{,}350.49-\$13{,}268.58=\$81.91[/latex] more. 35. If earning interest 5 more years (25 years total): 42. Continuous compounding: [latex]A=Pe^{rt}=12000e^{0.072\cdot 30}\approx \$104{,}053.65[/latex]. 43. Monthly compounding: [latex]A\approx 12000\left(1+\frac{0.072}{12}\right)^{12\cdot 30}\approx \$103{,}384.23[/latex]. This is about [latex]\$104{,}053.65-\$103{,}384.23=\$669.42[/latex] less than continuous compounding. 51. Using [latex]y=ab^x[/latex]: from [latex](0,3)[/latex], [latex]a=3[/latex]. From [latex](3,375)[/latex], [latex]375=3b^3\Rightarrow b^3=125\Rightarrow b=5[/latex]. So [latex]y=3\cdot 5^x[/latex]. 53. Using [latex]y=ab^x[/latex] through [latex](20,29.495)[/latex] and [latex](150,730.89)[/latex], a suitable model is [latex]y\approx 18(1.025)^x[/latex]. 55. Using [latex]y=ab^x[/latex] through [latex](11,310.035)[/latex] and [latex](25,356.3652)[/latex], a suitable model is [latex]y\approx 277.899(1.01)^x[/latex]. 61. Growth rate 9% per year from 2012 to 2020 (8 years): [latex]23900(1.09)^8\approx 47{,}622[/latex] foxes. 63. From 1985 to 2005 is 20 years: [latex]145000=110000(1+r)^{20}\Rightarrow r\approx 0.0139[/latex] (about 1.39% per year). 65. [latex]54000=P\left(1+\frac{0.082}{365}\right)^{365\cdot 5}\Rightarrow P\approx \$35{,}838.76[/latex]. 67. From 2000 to 2025 is 25 years, [latex]P=13500[/latex], [latex]r=0.0725[/latex]. 1. The horizontal asymptote tells what [latex]f(x)[/latex] approaches as [latex]x\to\infty[/latex] (and often also as [latex]x\to -\infty[/latex]). It describes the “end behavior” level the graph gets closer and closer to without reaching. 5. Reflect about the x-axis: [latex]-10^x[/latex]. Shift up 7: [latex]g(x)=-10^x+7[/latex]. 7. Starting with [latex]\left(\frac{1}{4}\right)^x[/latex]: left 2 gives [latex]\left(\frac{1}{4}\right)^{x+2}[/latex]; stretch by 4 gives [latex]4\left(\frac{1}{4}\right)^{x+2}[/latex]; reflect over x-axis gives [latex]-4\left(\frac{1}{4}\right)^{x+2}[/latex]; down 4 gives 11. 13. B 14. D 15. A 16. F 17. E 18. C 26. [latex]f(x)=2^{-x}[/latex]. Horizontal asymptote: [latex]y=0[/latex]. Domain: [latex](-\infty,\infty)[/latex]. Range: [latex](0,\infty)[/latex]. 27. [latex]h(x)=2^x+3[/latex]. Horizontal asymptote: [latex]y=3[/latex]. Domain: [latex](-\infty,\infty)[/latex]. Range: [latex](3,\infty)[/latex]. 28. [latex]f(x)=2^{x-2}[/latex]. Horizontal asymptote: [latex]y=0[/latex]. Domain: [latex](-\infty,\infty)[/latex]. Range: [latex](0,\infty)[/latex]. 39. [latex]y=-2^x+3[/latex]. 41. [latex]y=-2\cdot 3^x+7[/latex]. 47. [latex]116=\frac14\left(\frac18\right)^x\Rightarrow \left(\frac18\right)^x=464\Rightarrow x\approx -2.953[/latex]. 49. [latex]5=3\left(\frac12\right)^{x-1}-2\Rightarrow 7=3\left(\frac12\right)^{x-1}\Rightarrow x\approx -0.222[/latex]. 3. Use the definition of a logarithm: if [latex]\log_b(x)=y[/latex], then [latex]b^y=x[/latex]. So solving for [latex]x[/latex] gives [latex]x=b^y[/latex]. 7. [latex]\log_a(b)=c \iff a^c=b[/latex]. 9. [latex]\log_x(64)=y \iff x^y=64[/latex]. 11. [latex]\log_{15}(a)=b \iff 15^b=a[/latex]. 13. [latex]\log_{13}(142)=a \iff 13^a=142[/latex]. 15. [latex]\ln(w)=n \iff e^n=w[/latex]. 17. [latex]c^d=k \iff \log_c(k)=d[/latex]. 19. [latex]19^x=y \iff \log_{19}(y)=x[/latex]. 21. [latex]n^4=103 \iff \log_n(103)=4[/latex]. 23. [latex]y^x=\frac{39}{100} \iff \log_y\left(\frac{39}{100}\right)=x[/latex]. 25. [latex]e^k=h \iff \ln(h)=k[/latex]. 27. [latex]\log_2(x)=-3 \Rightarrow x=2^{-3}=\frac18[/latex]. 29. [latex]\log_3(x)=3 \Rightarrow x=3^3=27[/latex]. 31. [latex]\log_9(x)=\frac12 \Rightarrow x=9^{1/2}=3[/latex]. 33. [latex]\log_6(x)=-3 \Rightarrow x=6^{-3}=\frac{1}{216}[/latex]. 35. [latex]\ln(x)=2 \Rightarrow x=e^2[/latex]. 37. [latex]10^{\log(32)}=32[/latex]. 39. [latex]e^{\ln(1.06)}=1.06[/latex]. 41. [latex]e^{\ln(10.125)}+4=10.125+4=14.125[/latex]. 43. [latex]\log_6(\sqrt{6})=\log_6(6^{1/2})=\frac12[/latex]. 45. [latex]6\log_8(4)=6\cdot\frac{2}{3}=4[/latex]. 47. [latex]\log(0.001)=\log(10^{-3})=-3[/latex]. 49. [latex]2\log(100^{-3})=2\log(10^{-6})=2(-6)=-12[/latex]. 51. [latex]\ln(1)=0[/latex]. 53. [latex]25\ln\left(e^{2/5}\right)=25\cdot\frac{2}{5}=10[/latex]. 59. No. [latex]x=0[/latex] is not in the domain of [latex]f(x)=\log(x)[/latex] because logarithms require [latex]x>0[/latex]. So [latex]f(0)[/latex] is undefined (DNE). 66. [latex]\log\left(\frac{I_1}{I_2}\right)=M_1-M_2=9.0-6.1=2.9[/latex], so [latex]\frac{I_1}{I_2}=10^{2.9}\approx 794[/latex]. The 2011 quake was about 794 times as intense. 1. If two functions are inverses, their graphs are reflections across the line [latex]y=x[/latex]. So a point [latex](a,b)[/latex] on one graph corresponds to [latex](b,a)[/latex] on the inverse graph. 2. None. The range of a logarithmic function is all real numbers, and vertical translations do not change that (it remains [latex](-\infty,\infty)[/latex]). 3. Horizontal translations affect the domain because they move the vertical asymptote left or right (changing where the input becomes valid). 21. [latex]h(x)=\log_4(x-1)+1[/latex]. Domain: [latex](1,\infty)[/latex]. Range: [latex](-\infty,\infty)[/latex]. 23. [latex]g(x)=\ln(-x)-2[/latex]. Domain: [latex](-\infty,0)[/latex]. Range: [latex](-\infty,\infty)[/latex]. 25. [latex]h(x)=3\ln(x)-9[/latex]. Domain: [latex](0,\infty)[/latex]. Range: [latex](-\infty,\infty)[/latex]. 31. C 32. A 33. B 35. 37. 38. B 39. C 40. A 41. 43. 45. 51. Let [latex]u=x-1[/latex]. Then [latex]\log(u)=\ln(u)[/latex] implies [latex]u=1[/latex], so [latex]x=2[/latex]. 53. [latex]\ln(x-2)=-\ln(x+1)\Rightarrow \ln\big((x-2)(x+1)\big)=0\Rightarrow (x-2)(x+1)=1[/latex]. 55. [latex]\frac13\log(1-x)=\log(x+1)+\frac13[/latex] has solution [latex]x\approx -0.472[/latex] (nearest thousandth).
Semi-annually: [latex]\$15{,}859.97-\$13{,}268.58=\$2{,}591.39[/latex] more.
Weekly: [latex]\$15{,}982.44-\$13{,}350.49=\$2{,}631.95[/latex] more.
Value in 2010 (25 years after 1985): [latex]110000(1+r)^{25}\approx \$155{,}368.09[/latex].
Monthly: [latex]A\approx 13500\left(1+\frac{0.0725}{12}\right)^{12\cdot 25}\approx \$82{,}247.78[/latex].
Continuous: [latex]A\approx 13500e^{0.0725\cdot 25}\approx \$82{,}697.53[/latex].
Continuous earns about [latex]\$82{,}697.53-\$82{,}247.78=\$449.75[/latex] more.Graphs of Exponential Functions
3. Reflect about the y-axis: [latex]3^{-x}[/latex]. Stretch vertically by 4: [latex]g(x)=4\cdot 3^{-x}[/latex].
y-intercept: [latex]g(0)=4[/latex]. Domain: [latex](-\infty,\infty)[/latex]. Range: [latex](0,\infty)[/latex].
y-intercept: [latex]g(0)=-1+7=6[/latex]. Domain: [latex](-\infty,\infty)[/latex]. Range: [latex](-\infty,7)[/latex].
[latex]g(x)=-4\left(\frac{1}{4}\right)^{x+2}-4[/latex].
y-intercept: [latex]g(0)=-4\left(\frac{1}{4}\right)^2-4=-\frac{17}{4}[/latex]. Domain: [latex](-\infty,\infty)[/latex]. Range: [latex](-\infty,-4)[/latex].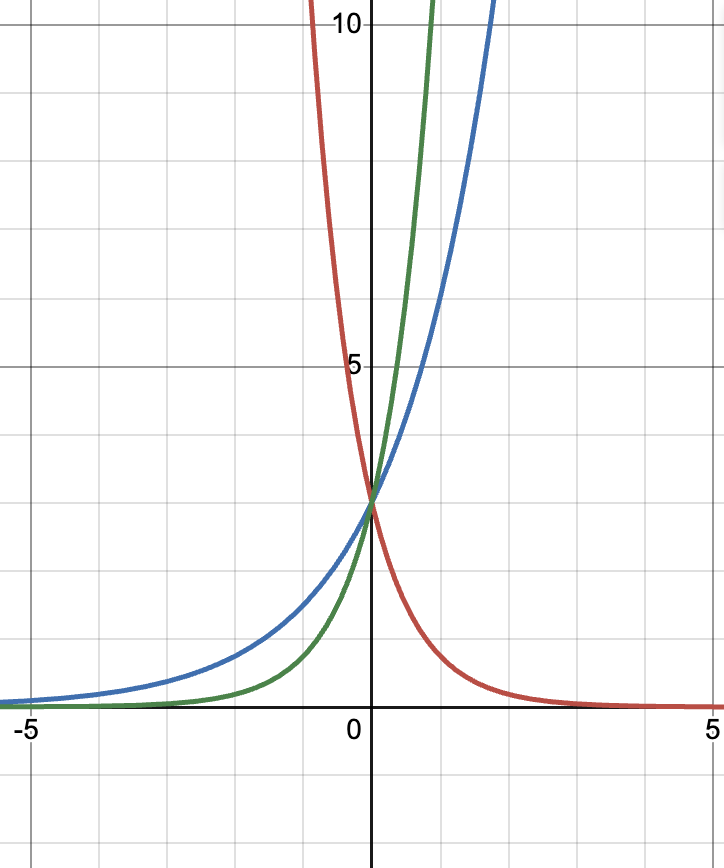
Logarithmic Functions
Graphs of Logarithmic Functions
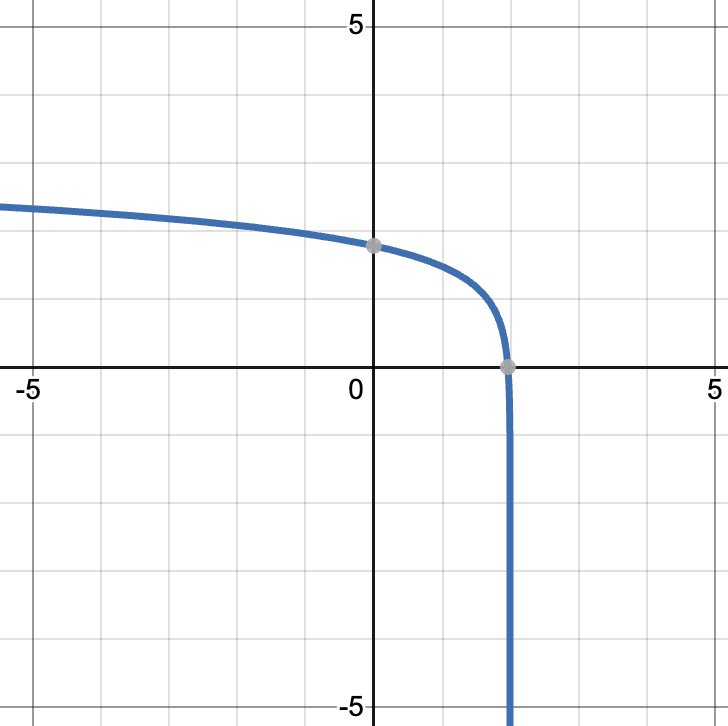
x-intercept: [latex]\log_4(x-1)+1=0\Rightarrow x-1=\frac14\Rightarrow x=\frac54[/latex]. y-intercept: DNE.
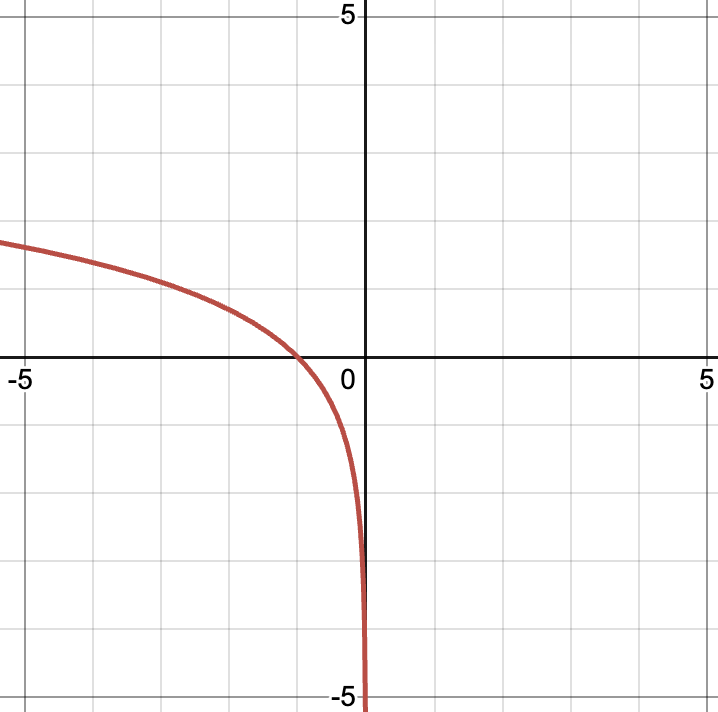
x-intercept: [latex]\ln(-x)-2=0\Rightarrow -x=e^2\Rightarrow x=-e^2[/latex]. y-intercept: DNE.
x-intercept: [latex]3\ln(x)-9=0\Rightarrow \ln(x)=3\Rightarrow x=e^3[/latex]. y-intercept: DNE.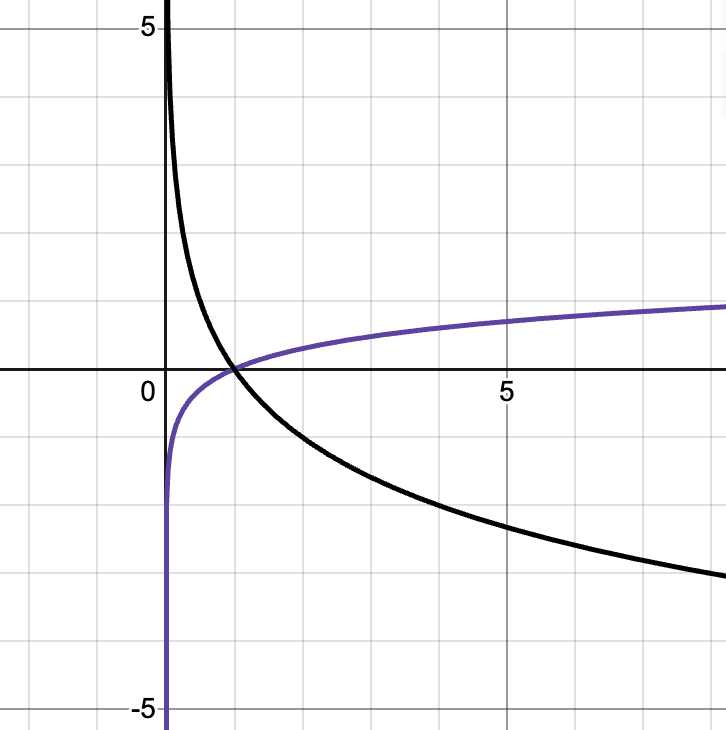
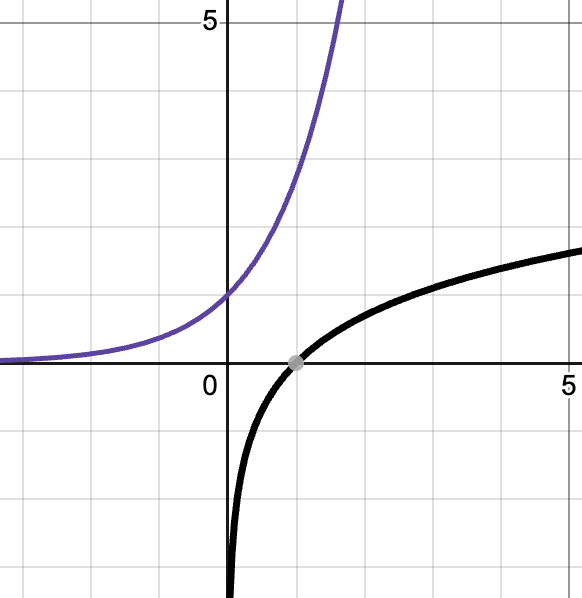
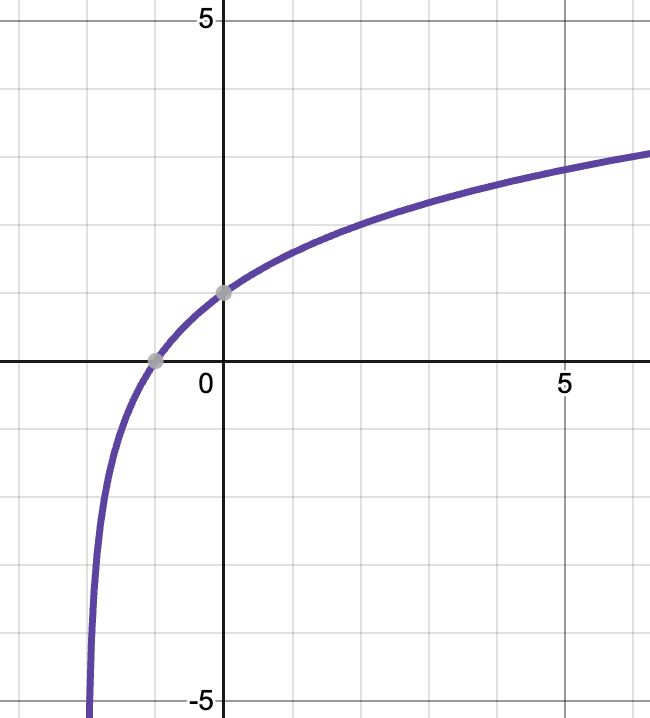
[latex]x=\frac{1+\sqrt{13}}{2}\approx 2.303[/latex].