Exponential and Logarithmic Equations Get Stronger Answer Key

Giselle Miller

Exponential and Logarithmic Equations Get Stronger Answer Key

Exponential and Logarithmic Equations: Get Stronger Key

Logarithmic Properties

3. [latex]{\mathrm{log}}_{b}\left(2\right)+{\mathrm{log}}_{b}\left(7\right)+{\mathrm{log}}_{b}\left(x\right)+{\mathrm{log}}_{b}\left(y\right)[/latex]

5. [latex]{\mathrm{log}}_{b}\left(13\right)-{\mathrm{log}}_{b}\left(17\right)[/latex]

7. [latex]-k\mathrm{ln}\left(4\right)[/latex]

9. [latex]\mathrm{ln}\left(7xy\right)[/latex]

11. [latex]{\mathrm{log}}_{b}\left(4\right)[/latex]

13. [latex]{\text{log}}_{b}\left(7\right)[/latex]

15. [latex]15\mathrm{log}\left(x\right)+13\mathrm{log}\left(y\right)-19\mathrm{log}\left(z\right)[/latex]

17. [latex]\frac{3}{2}\mathrm{log}\left(x\right)-2\mathrm{log}\left(y\right)[/latex]

19. [latex]\frac{8}{3}\mathrm{log}\left(x\right)+\frac{14}{3}\mathrm{log}\left(y\right)[/latex]

21. [latex]\mathrm{ln}\left(2{x}^{7}\right)[/latex]

23. [latex]\mathrm{log}\left(\frac{x{z}^{3}}{\sqrt{y}}\right)[/latex]

27. [latex]{\mathrm{log}}_{11}\left(5\right)=\frac{{\mathrm{log}}_{5}\left(5\right)}{{\mathrm{log}}_{5}\left(11\right)}=\frac{1}{b}[/latex]

29. [latex]{\mathrm{log}}_{11}\left(\frac{6}{11}\right)=\frac{{\mathrm{log}}_{5}\left(\frac{6}{11}\right)}{{\mathrm{log}}_{5}\left(11\right)}=\frac{{\mathrm{log}}_{5}\left(6\right)-{\mathrm{log}}_{5}\left(11\right)}{{\mathrm{log}}_{5}\left(11\right)}=\frac{a-b}{b}=\frac{a}{b}-1[/latex]

31. 3

33. 2.81359

35. 0.93913

37. –2.23266

39. x = 4; By the quotient rule: [latex]{\mathrm{log}}_{6}\left(x+2\right)-{\mathrm{log}}_{6}\left(x - 3\right)={\mathrm{log}}_{6}\left(\frac{x+2}{x - 3}\right)=1[/latex].

Rewriting as an exponential equation and solving for x:

[latex]\begin{cases}{6}^{1}\hfill & =\frac{x+2}{x - 3}\hfill \\ 0\hfill & =\frac{x+2}{x - 3}-6\hfill \\ 0\hfill & =\frac{x+2}{x - 3}-\frac{6\left(x - 3\right)}{\left(x - 3\right)}\hfill \\ 0\hfill & =\frac{x+2 - 6x+18}{x - 3}\hfill \\ 0\hfill & =\frac{x - 4}{x - 3}\hfill \\ \text{ }x\hfill & =4\hfill \end{cases}[/latex]

Checking, we find that [latex]{\mathrm{log}}_{6}\left(4+2\right)-{\mathrm{log}}_{6}\left(4 - 3\right)={\mathrm{log}}_{6}\left(6\right)-{\mathrm{log}}_{6}\left(1\right)[/latex] is defined, so x = 4.

Exponential and Logarithmic Equations

2. An extraneous solution occurs when solving the equation results in a value that does not satisfy the original equation. It can be recognized by substituting the solution back into the original equation and seeing that it makes the equation false or violates a domain restriction (for example, giving a negative input to a logarithm or an even root, or causing division by zero).

3. The one-to-one property can be used if both sides of the equation can be rewritten as a single logarithm with the same base. If so, the arguments can be set equal to each other, and the resulting equation can be solved algebraically. The one-to-one property cannot be used when each side of the equation cannot be rewritten as a single logarithm with the same base.

5. [latex]x=-\frac{1}{3}[/latex]

7. n = –1

9. [latex]b=\frac{6}{5}[/latex]

11. x = 10

13. No solution

15. [latex]p=\mathrm{log}\left(\frac{17}{8}\right)-7[/latex]

21. [latex]x=\mathrm{ln}12[/latex]

27. [latex]x=\mathrm{ln}\left(3\right)[/latex]

31. n = 49

33. [latex]k=\frac{1}{36}[/latex]

35. [latex]x=\frac{9-e}{8}[/latex]

37. n = 1

39. No solution

41. No solution

43. [latex]x=\pm \frac{10}{3}[/latex]

51. x = 9
Graph of log_9(x)-5=y and y=-4.

53. [latex]x=\frac{{e}^{2}}{3}\approx 2.5[/latex]
Graph of ln(3x)=y and y=2.

55. x = –5
Graph of log(4)+log(-5x)=y and y=2.

57. [latex]x=\frac{e+10}{4}\approx 3.2[/latex]
Graph of ln(4x-10)-6=y and y=-5.

59. No solution
Graph of log_11(-2x^2-7x)=y and y=log_11(x-2).

61. [latex]x=\frac{11}{5}\approx 2.2[/latex]
Graph of log_9(3-x)=y and y=log_9(4x-8).

65. about $27,710.24

Graph of f(x)=6500e^(0.0725x) with the labeled point at (20, 27710.24).

67. about 5 years

69. [latex]\frac{\mathrm{ln}\left(17\right)}{5}\approx 0.567[/latex]

71. [latex]x=\frac{\mathrm{log}\left(38\right)+5\mathrm{log}\left(3\right)\text{ }}{4\mathrm{log}\left(3\right)}\approx 2.078[/latex]

73. [latex]x\approx 2.2401[/latex]

75. [latex]x\approx -44655.7143[/latex]

77. about 5.83

81. [latex]t=\mathrm{ln}\left({\left(\frac{T-{T}_{s}}{{T}_{0}-{T}_{s}}\right)}^{-\frac{1}{k}}\right)[/latex]

Exponential and Logarithmic Models

1. Half-life is a measure of decay and is thus associated with exponential decay models. The half-life of a substance or quantity is the amount of time it takes for half of the initial amount of that substance or quantity to decay.

7. [latex]f\left(0\right)\approx 16.7[/latex]; The amount initially present is about 16.7 units.

9. 150

11. exponential; [latex]f\left(x\right)={1.2}^{x}[/latex]

13. logarithmic
Graph of the question’s table.

15. logarithmic
Graph of the question’s table.

17.
Graph of P(t)=1000/(1+9e^(-0.6t))

21. about 7.3 years

23. 4 half-lives; 8.18 minutes

25. [latex]\begin{cases}\text{ }M=\frac{2}{3}\mathrm{log}\left(\frac{S}{{S}_{0}}\right)\hfill \\ \mathrm{log}\left(\frac{S}{{S}_{0}}\right)=\frac{3}{2}M\hfill \\ \text{ }\frac{S}{{S}_{0}}={10}^{\frac{3M}{2}}\hfill \\ \text{ }S={S}_{0}{10}^{\frac{3M}{2}}\hfill \end{cases}//[/latex]

28. 2 hours.

29. [latex]A=125{e}^{\left(-0.3567t\right)};A\approx 43[/latex] mg

31. about 60 days

32. [latex]A(t)=0.5(0.9885)^t[/latex]. After 60 days, [latex]A(60)\approx 0.3[/latex] grams.

33. [latex]f\left(t\right)=250{e}^{\left(-0.00914t\right)}[/latex]; half-life: about [latex]\text{76}[/latex] minutes

35. [latex]r\approx -0.0667[/latex], So the hourly decay rate is about 6.67%

37. [latex]f\left(t\right)=1350{e}^{\left(0.03466t\right)}[/latex]; after 3 hours: [latex]P\left(180\right)\approx 691,200[/latex]

40. [latex]T(t)=69+31e^{\left(\frac{1}{15}\ln\left(\frac{26}{31}\right)\right)t}[/latex].

41. about 88 minutes

Fitting Exponential Models to Data

4. A scatterplot that is best described by a logarithmic model would show a rapid increase or decrease at first, followed by a gradual leveling off as the input values increase. The data points would form a curve that rises (or falls) quickly and then flattens.

6. E

7. C

8. A

9. B

10. D

11. [latex]P\left(0\right)=22[/latex] ; 175

13. [latex]p\approx 2.67[/latex]

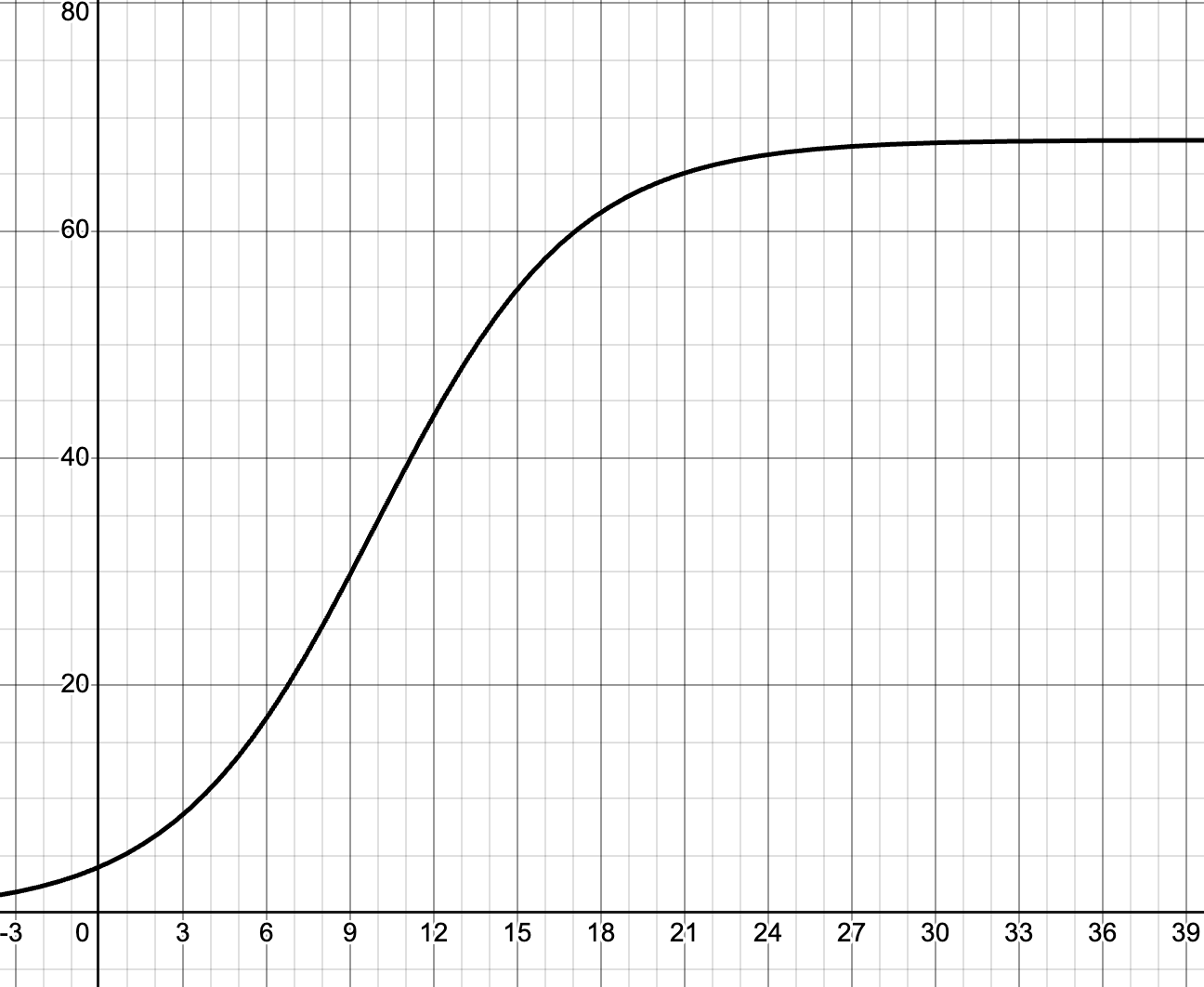
16. The graph is a logistic growth function. It increases slowly at first, then more rapidly, and finally levels off around 27 months near the max capacity of 68. For small x-values near 0, the y-values are close to 0. Around x equals 6, the y-value is about 15. Around x equals 12, the y-value is about 45. Around x equals 18, the y-value is about 60.

17. 4 koi

18. 6.8 months

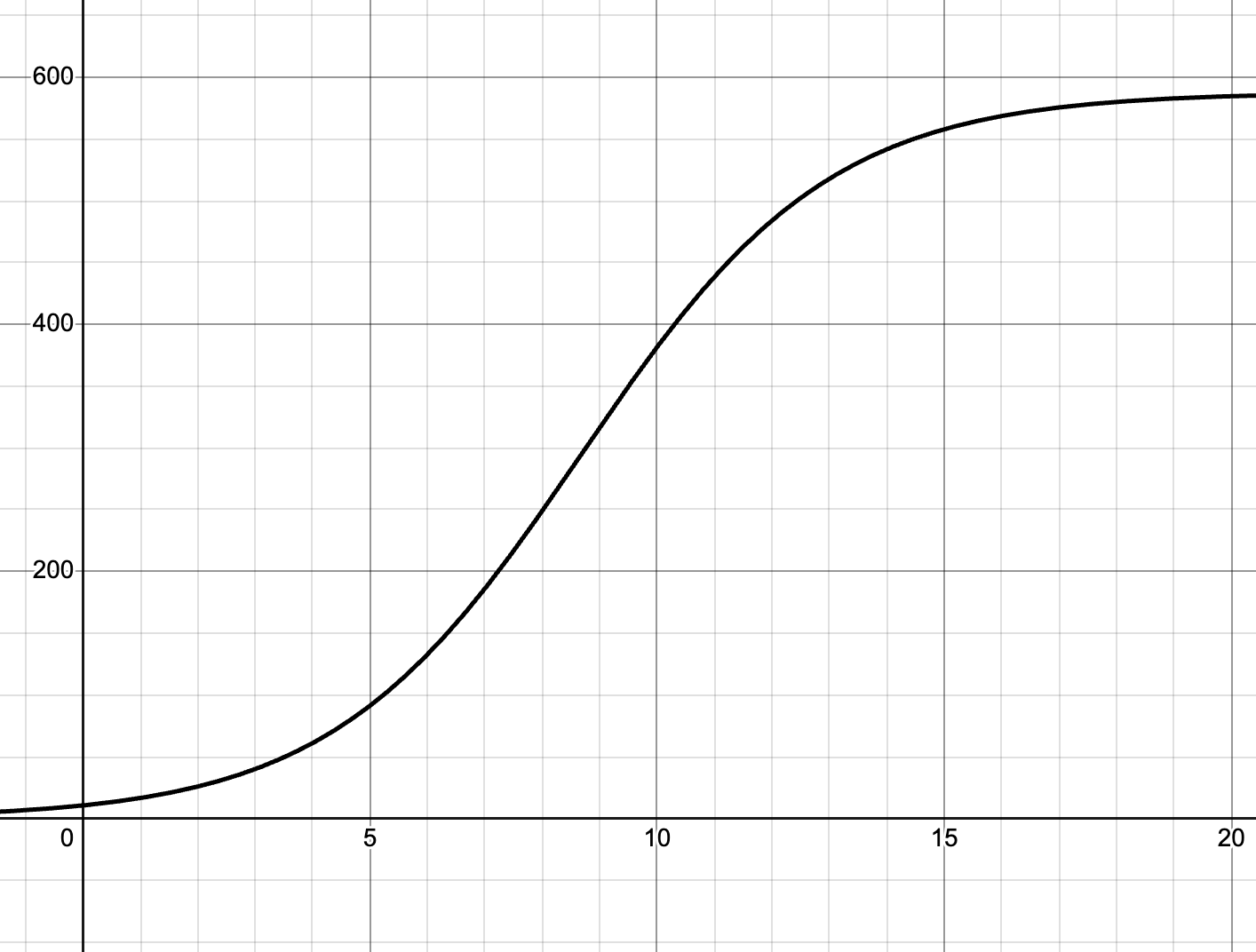
20. The graph is a logistic growth function. It increases slowly at first, then more rapidly, and then levels off as x increases. The graph has approximate values: At x equals 0, y is close to 0. At x equals 5, y is about 80. At x equals 10, y is about 400. At x equals 15, y is about 550. At x equals 20, y is about 580. The graph approaches a horizontal asymptote at y equals 588 but does not reach it.