Rational Functions: Get Stronger Key
Rational Functions
Solutions to Odd-Numbered Exercises
1. The rational function will be represented by a quotient of polynomial functions.
3. The numerator and denominator must have a common factor.
5. Yes. The numerator of the formula of the functions would have only complex roots and/or factors common to both the numerator and denominator.
7. [latex]\text{All reals }x\ne -1, 1[/latex]
9. [latex]\text{All reals }x\ne -1, -2, 1, 2[/latex]
11. V.A. at [latex]x=-\frac{2}{5}[/latex]; H.A. at [latex]y=0[/latex]; Domain is all reals [latex]x\ne -\frac{2}{5}[/latex]
13. V.A. at [latex]x=4, -9[/latex]; H.A. at [latex]y=0[/latex]; Domain is all reals [latex]x\ne 4, -9[/latex]
15. V.A. at [latex]x=0, 4, -4[/latex]; H.A. at [latex]y=0[/latex]; Domain is all reals [latex]x\ne 0,4, -4[/latex]
17. V.A. at [latex]x=-5[/latex]; H.A. at [latex]y=0[/latex]; Domain is all reals [latex]x\ne 5,-5[/latex]
19. V.A. at [latex]x=\frac{1}{3}[/latex]; H.A. at [latex]y=-\frac{2}{3}[/latex]; Domain is all reals [latex]x\ne \frac{1}{3}[/latex].
21. none
23. [latex]x\text{-intercepts none, }y\text{-intercept }\left(0,\frac{1}{4}\right)[/latex]
25. Local behavior: [latex]x\to -{\frac{1}{2}}^{+},f\left(x\right)\to -\infty ,x\to -{\frac{1}{2}}^{-},f\left(x\right)\to \infty[/latex]
End behavior: [latex]x\to \pm \infty ,f\left(x\right)\to \frac{1}{2}[/latex]
27. Local behavior: [latex]x\to {6}^{+},f\left(x\right)\to -\infty ,x\to {6}^{-},f\left(x\right)\to \infty[/latex], End behavior: [latex]x\to \pm \infty ,f\left(x\right)\to -2[/latex]
29. Local behavior: [latex]x\to -{\frac{1}{3}}^{+},f\left(x\right)\to \infty ,x\to -{\frac{1}{3}}^{-}[/latex], [latex]f\left(x\right)\to -\infty ,x\to {\frac{5}{2}}^{-},f\left(x\right)\to \infty ,x\to {\frac{5}{2}}^{+}[/latex] , [latex]f\left(x\right)\to -\infty[/latex]
End behavior: [latex]x\to \pm \infty\\[/latex], [latex]f\left(x\right)\to \frac{1}{3}[/latex]
31. [latex]y=2x+4[/latex]
33. [latex]y=2x[/latex]
35. [latex]V.A.\text{ }x=0,H.A.\text{ }y=2[/latex]
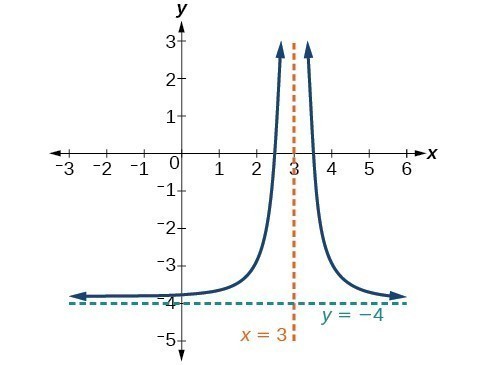
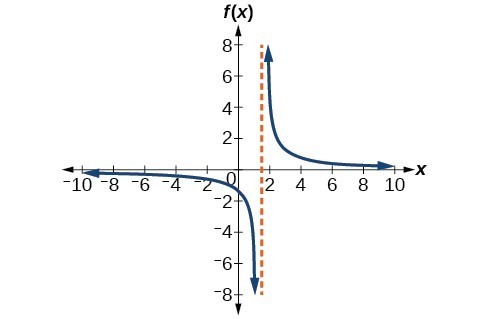
37. [latex]V.A.\text{ }x=2,\text{ }H.A.\text{ }y=0[/latex]
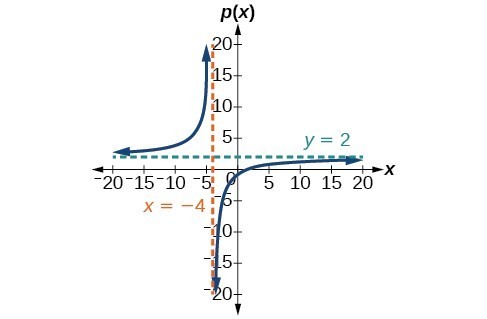
39. [latex]V.A.\text{ }x=-4,\text{ }H.A.\text{ }y=2;\left(\frac{3}{2},0\right);\left(0,-\frac{3}{4}\right)[/latex]
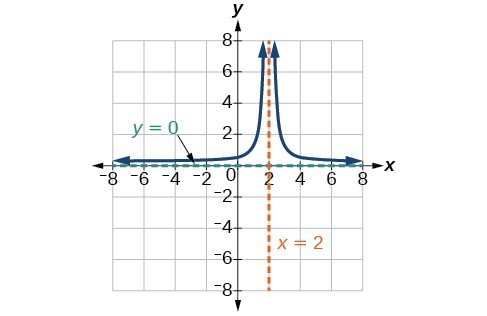
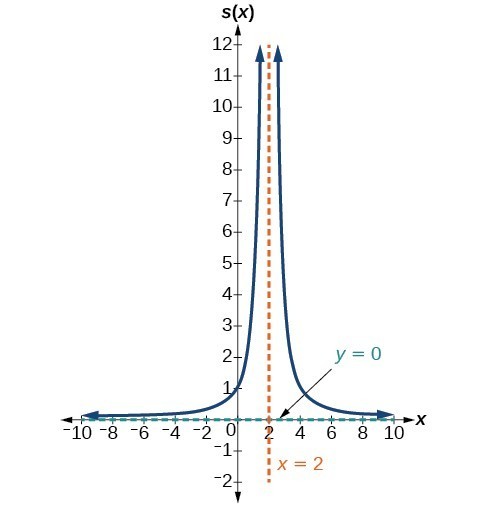
41. [latex]V.A.\text{ }x=2,\text{ }H.A.\text{ }y=0,\text{ }\left(0,1\right)[/latex]
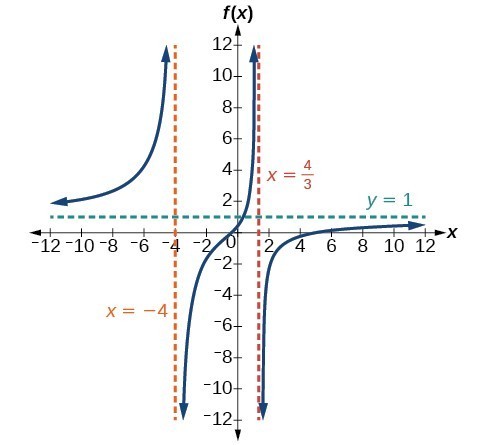
43. [latex]V.A.\text{ }x=-4,\text{ }x=\frac{4}{3},\text{ }H.A.\text{ }y=1;\left(5,0\right);\left(-\frac{1}{3},0\right);\left(0,\frac{5}{16}\right)[/latex]
45. [latex]V.A.\text{ }x=-1,\text{ }H.A.\text{ }y=1;\left(-3,0\right);\left(0,3\right)[/latex]
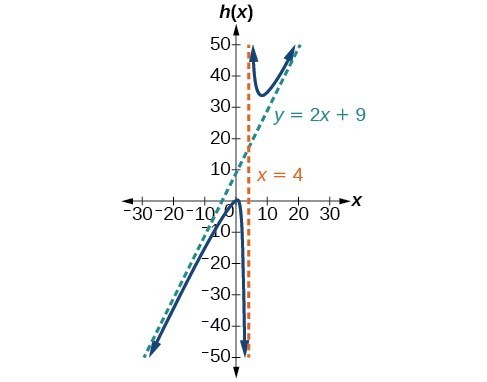
47. [latex]V.A.\text{ }x=4,\text{ }S.A.\text{ }y=2x+9;\left(-1,0\right);\left(\frac{1}{2},0\right);\left(0,\frac{1}{4}\right)[/latex]
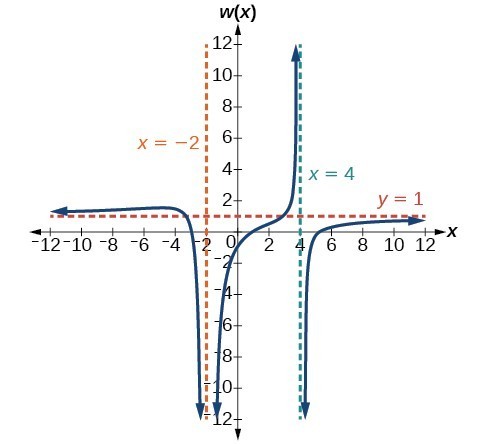
49. [latex]V.A.\text{ }x=-2,\text{ }x=4,\text{ }H.A.\text{ }y=1,\left(1,0\right);\left(5,0\right);\left(-3,0\right);\left(0,-\frac{15}{16}\right)[/latex]
51. [latex]y=50\frac{{x}^{2}-x - 2}{{x}^{2}-25}[/latex]
53. [latex]y=7\frac{{x}^{2}+2x - 24}{{x}^{2}+9x+20}[/latex]
55. [latex]y=\frac{1}{2}\frac{{x}^{2}-4x+4}{x+1}[/latex]
57. [latex]y=4\frac{x - 3}{{x}^{2}-x - 12}[/latex]
59. [latex]y=-9\frac{x - 2}{{x}^{2}-9}[/latex]
61. [latex]y=\frac{1}{3}\frac{{x}^{2}+x - 6}{x - 1}[/latex]
63. [latex]y=-6\frac{{\left(x - 1\right)}^{2}}{\left(x+3\right){\left(x - 2\right)}^{2}}[/latex]
65.
| x | 2.01 | 2.001 | 2.0001 | 1.99 | 1.999 |
| y | 100 | 1,000 | 10,000 | –100 | –1,000 |
| x | 10 | 100 | 1,000 | 10,000 | 100,000 |
| y | .125 | .0102 | .001 | .0001 | .00001 |
Vertical asymptote [latex]x=2[/latex], Horizontal asymptote [latex]y=0[/latex]
67.
| x | –4.1 | –4.01 | –4.001 | –3.99 | –3.999 |
| y | 82 | 802 | 8,002 | –798 | –7998 |
| x | 10 | 100 | 1,000 | 10,000 | 100,000 |
| y | 1.4286 | 1.9331 | 1.992 | 1.9992 | 1.999992 |
Vertical asymptote [latex]x=-4[/latex], Horizontal asymptote [latex]y=2[/latex]
69.
| x | –.9 | –.99 | –.999 | –1.1 | –1.01 |
| y | 81 | 9,801 | 998,001 | 121 | 10,201 |
| x | 10 | 100 | 1,000 | 10,000 | 100,000 |
| y | .82645 | .9803 | .998 | .9998 |
Vertical asymptote [latex]x=-1[/latex], Horizontal asymptote [latex]y=1[/latex]
71. [latex]\left(\frac{3}{2},\infty \right)[/latex]
73. [latex]\left(-2,1\right)\cup \left(4,\infty \right)[/latex]
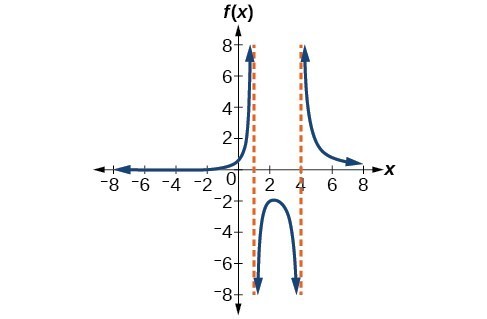
75. [latex]\left(2,4\right)[/latex]
77. [latex]\left(2,5\right)[/latex]
79. [latex]\left(-1,\text{1}\right)[/latex]
81. [latex]C\left(t\right)=\frac{8+2t}{300+20t}[/latex]
83. After about 6.12 hours.
85. [latex]A\left(x\right)=50{x}^{2}+\frac{800}{x}[/latex]. 2 by 2 by 5 feet.
87. [latex]A\left(x\right)=\pi {x}^{2}+\frac{100}{x}[/latex]. Radius = 2.52 meters.
Modeling Using Variation
Solutions to Odd-Numbered Exercises
1. The graph will have the appearance of a power function.
3. No. Multiple variables may jointly vary.
5. [latex]y=5{x}^{2}[/latex]
7. [latex]y=10{x}^{3}[/latex]
9. [latex]y=6{x}^{4}[/latex]
11. [latex]y=\frac{18}{{x}^{2}}[/latex]
13. [latex]y=\frac{81}{{x}^{4}}[/latex]
15. [latex]y=\frac{20}{\sqrt[3]{x}}[/latex]
17. [latex]y=10xzw[/latex]
19. [latex]y=10x\sqrt{z}[/latex]
21. [latex]y=4\frac{xz}{w}[/latex]
23. [latex]y=40\frac{xz}{\sqrt{w}{t}^{2}}[/latex]
25. [latex]y=256[/latex]
27. [latex]y=6[/latex]
29. [latex]y=6[/latex]
31. [latex]y=27[/latex]
33. [latex]y=3[/latex]
35. [latex]y=18[/latex]
37. [latex]y=90[/latex]
39. [latex]y=\frac{81}{2}[/latex]
41. [latex]y=\frac{3}{4}{x}^{2}[/latex]
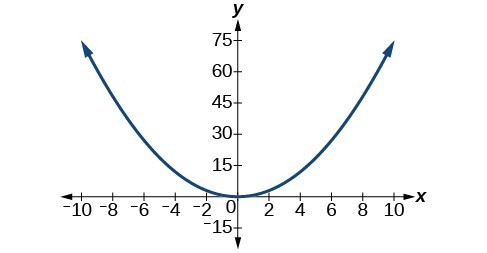
43. [latex]y=\frac{1}{3}\sqrt{x}[/latex]
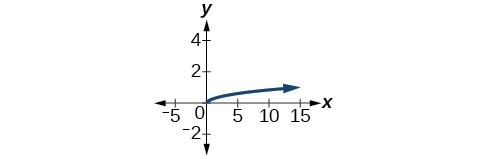
45. [latex]y=\frac{4}{{x}^{2}}[/latex]
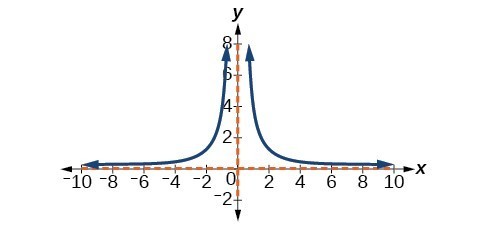
47. 1.89 years
49. 0.61 years
51. 3 seconds
53. 48 inches
55. 49.75 pounds
57. 33.33 amperes
59. 2.88 inches