Linear Functions

1. Terry starts at an elevation of 3000 feet and descends 70 feet per second.

3. 3 miles per hour

5. [latex]d\left(t\right)=100 - 10t[/latex]

7. Yes.

9. No.

11. No.

13. No.

15. Increasing.

17. Decreasing.

19. Decreasing.

21. Increasing.

23. Decreasing.

25. 3

27. [latex]-\frac{1}{3}[/latex]

29. [latex]\frac{4}{5}[/latex]

31. [latex]f\left(x\right)=-\frac{1}{2}x+\frac{7}{2}[/latex]

33. [latex]y=2x+3[/latex]

35. [latex]y=-\frac{1}{3}x+\frac{22}{3}[/latex]

37. [latex]y=\frac{4}{5}x+4[/latex]

39. [latex]-\frac{5}{4}[/latex]

41. [latex]y=\frac{2}{3}x+1[/latex]

43. [latex]y=-2x+3[/latex]

45. [latex]y=3[/latex]

47. Linear, [latex]g\left(x\right)=-3x+5[/latex]

49. Linear, [latex]f\left(x\right)=5x - 5[/latex]

51. Linear, [latex]g\left(x\right)=-\frac{25}{2}x+6[/latex]

53. Linear, [latex]f\left(x\right)=10x - 24[/latex]

55. [latex]f\left(x\right)=-58x+17.3[/latex]

57.

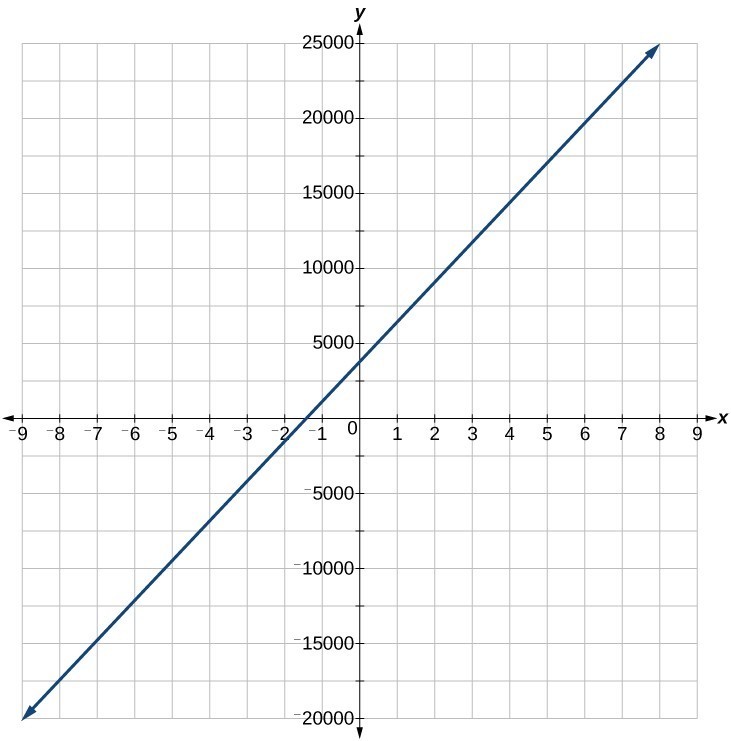
59. a. [latex]a=11,900[/latex] ; [latex]b=1001.1[/latex] b. [latex]q\left(p\right)=1000p - 100[/latex]

61.

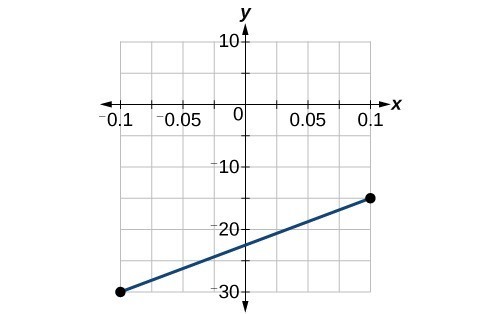
63. [latex]x=-\frac{16}{3}[/latex]

65. [latex]x=a[/latex]

67. [latex]y=\frac{d}{c-a}x-\frac{ad}{c-a}[/latex]

69. $45 per training session.

71. The rate of change is 0.1. For every additional minute talked, the monthly charge increases by $0.1 or 10 cents. The initial value is 24. When there are no minutes talked, initially the charge is $24.

73. The slope is –400. This means for every year between 1960 and 1989, the population dropped by 400 per year in the city.

75. c

Graphs of Linear Functions

1. The slopes are equal; y-intercepts are not equal.

3. The point of intersection is [latex]\left(a,a\right)[/latex]. This is because for the horizontal line, all of the y coordinates are a and for the vertical line, all of the x coordinates are a. The point of intersection will have these two characteristics.

5. First, find the slope of the linear function. Then take the negative reciprocal of the slope; this is the slope of the perpendicular line. Substitute the slope of the perpendicular line and the coordinate of the given point into the equation [latex]y=mx+b[/latex] and solve for b. Then write the equation of the line in the form [latex]y=mx+b[/latex] by substituting in m and b.

7. neither parallel or perpendicular

9. perpendicular

11. parallel

13. [latex]\left(-2\text{, }0\right)[/latex] ; [latex]\left(0\text{, 4}\right)[/latex]

15. [latex]\left(\frac{1}{5}\text{, }0\right)[/latex] ; [latex]\left(0\text{, 1}\right)[/latex]

17. [latex]\left(8\text{, }0\right)[/latex] ; [latex]\left(0\text{, }28\right)[/latex]

19. [latex]\text{Line 1}: m=8 \text{ Line 2}: m=-6 \text{Neither}[/latex]

21. [latex]\text{Line 1}: m=-\frac{1}{2} \text{ Line 2}: m=2 \text{Perpendicular}[/latex]

23. [latex]\text{Line 1}: m=-2 \text{ Line 2}: m=-2 \text{Parallel}[/latex]

25. [latex]g\left(x\right)=3x - 3[/latex]

27. [latex]p\left(t\right)=-\frac{1}{3}t+2[/latex]

29. [latex]\left(-2,1\right)[/latex]

31. [latex]\left(-\frac{17}{5},\frac{5}{3}\right)[/latex]

33. F

35. C

37. A

39.

41.

43.

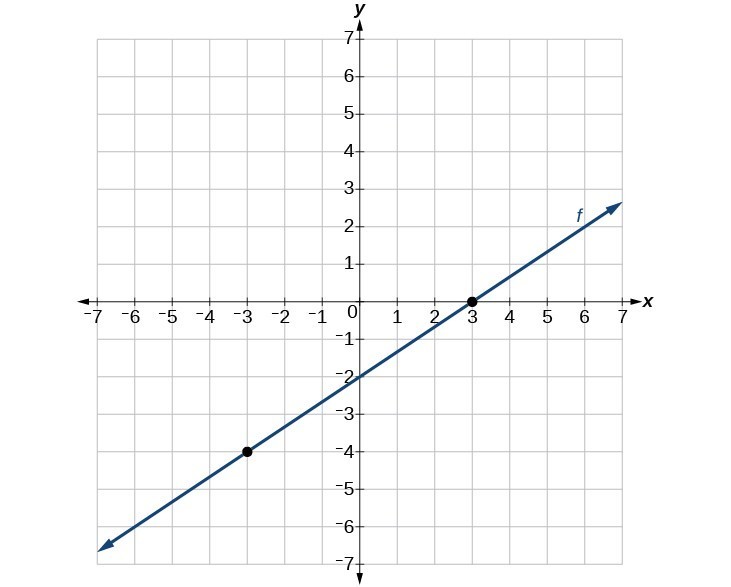
45.

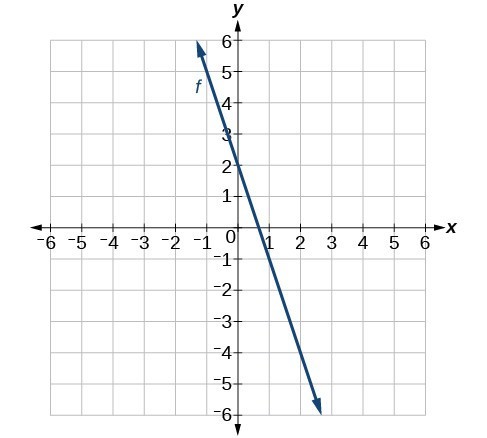
47.

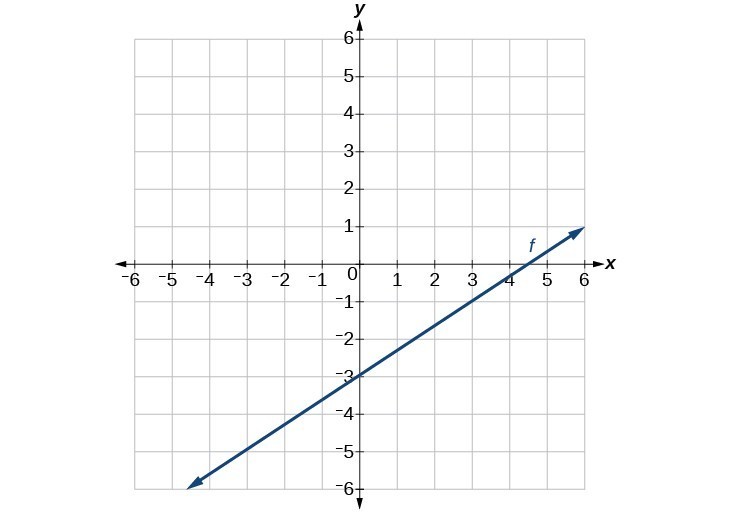
49.

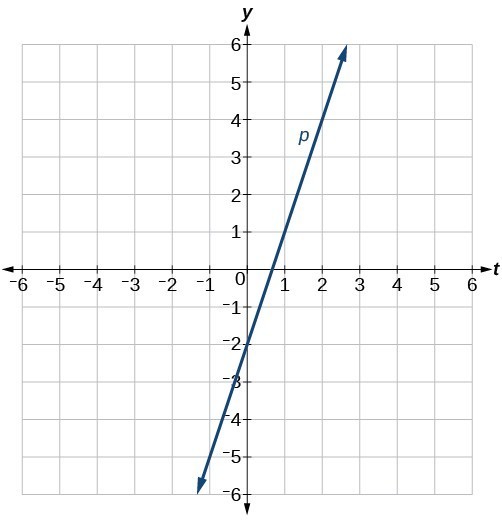
51.

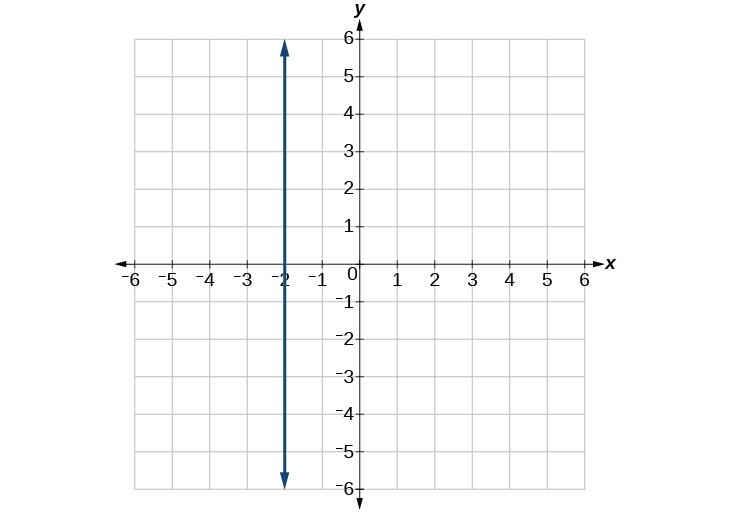
53.

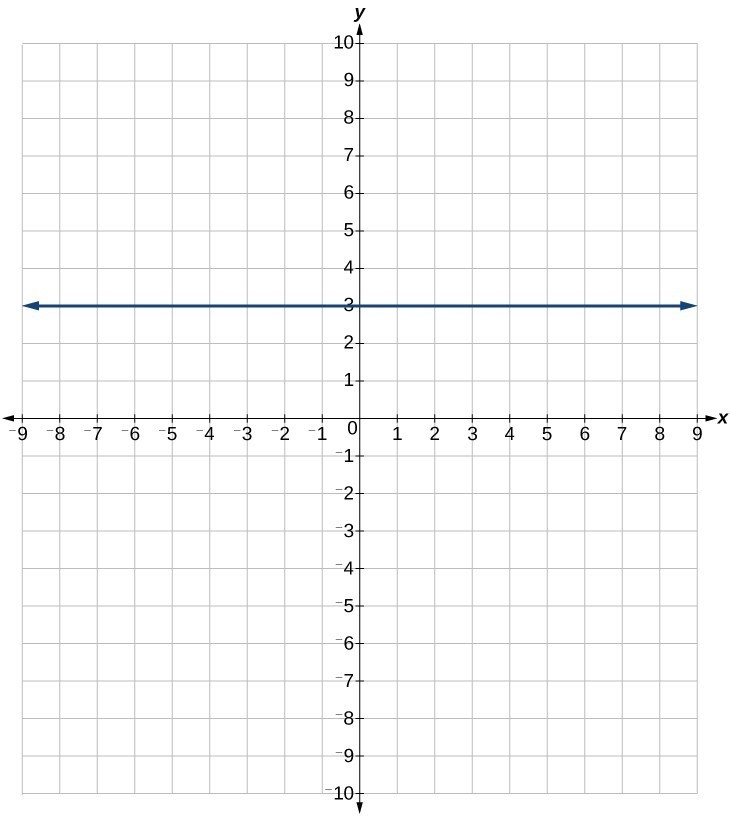
55.

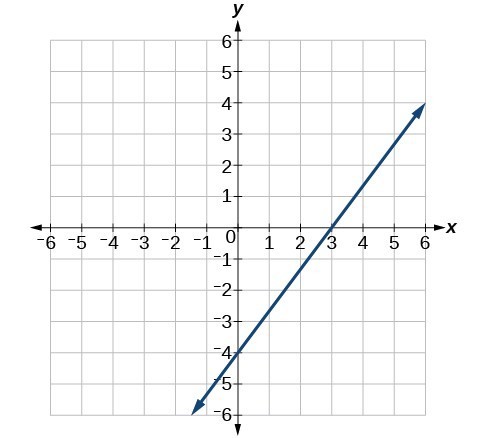
57.

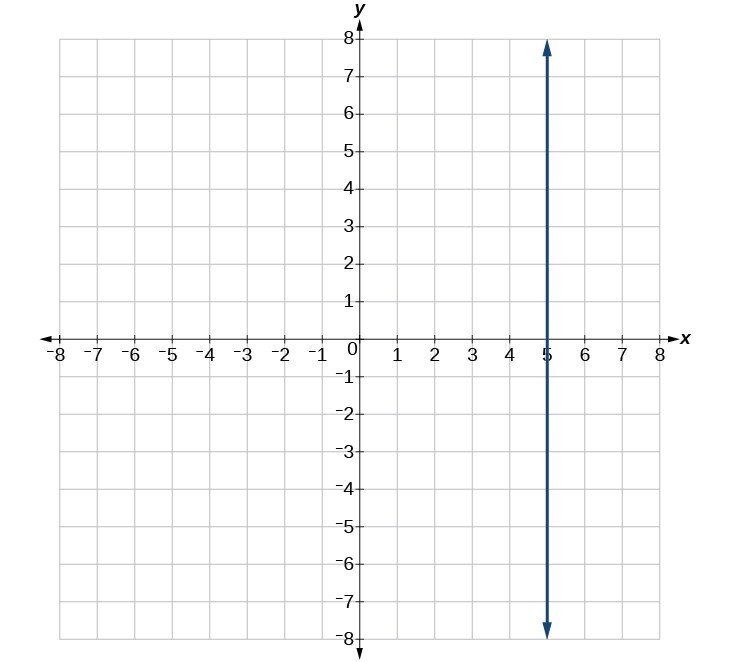
59. [latex]g\left(x\right)=0.75x - 5.5\text{}[/latex] 0.75 [latex]\left(0,-5.5\right)[/latex]

61. [latex]y=3[/latex]

63. [latex]x=-3[/latex]

65. no point of intersection

67. [latex]\left(\text{2},\text{ 7}\right)[/latex]

69. [latex]\left(-10,\text{ }-5\right)[/latex]

71. [latex]y=100x - 98[/latex]

73. [latex]x<\frac{1999}{201}x>\frac{1999}{201}[/latex]

75. Less than 3000 texts

Modeling with Linear Functions

1. Determine the independent variable. This is the variable upon which the output depends.

3. To determine the initial value, find the output when the input is equal to zero.

5. 6 square units

7. 20.012 square units

9. 2,300

11. 64,170

13. [latex]P\left(t\right)=75,000+2500t[/latex]

15. (–30, 0) Thirty years before the start of this model, the town had no citizens. (0, 75,000) Initially, the town had a population of 75,000.

17. Ten years after the model began.

19. [latex]W\left(t\right)=\text{7}.\text{5}t+0.\text{5}[/latex]

21. (–15, 0): The x-intercept is not a plausible set of data for this model because it means the baby weighed 0 pounds 15 months prior to birth. (0, 7.5): The baby weighed 7.5 pounds at birth.

23. At age 5.8 months.

25. [latex]C\left(t\right)=12,025 - 205t[/latex]

27. (58.7, 0): In roughly 59 years, the number of people inflicted with the common cold would be 0. (0, 12,025): Initially there were 12,025 people afflicted by the common cold.

29. 2064

31. [latex]y=-2t+180[/latex]

33. In 2070, the company’s profit will be zero.

35. [latex]y=30t - 300[/latex]

37. (10, 0) In 1990, the profit earned zero profit.

39. Hawaii

41. During the year 1933

43. $105,620

45.

a. 696 people
b. 4 years
c. 174 people per year
d. 305 people
e. [latex]P\left(t\right)=305+174t[/latex]
f. 2219 people

47.

a. [latex]C\left(x\right)=0.15x+10[/latex]
b. The flat monthly fee is $10 and there is an additional $0.15 fee for each additional minute used
c. $113.05

49.

a. [latex]P\left(t\right)=190t+4360[/latex]
b. 6640 moose

51.

a. [latex]R\left(t\right)=16 - 2.1t[/latex]
b. 5.5 billion cubic feet
c. During the year 2017

53. More than 133 minutes

55. More than $42,857.14 worth of jewelry

57. $66,666.67

Fitting Linear Models to Data

1. When our model no longer applies, after some value in the domain, the model itself doesn’t hold.

3. We predict a value outside the domain and range of the data.

5. The closer the number is to 1, the less scattered the data, the closer the number is to 0, the more scattered the data.

7. 61.966 years

9. No

11. No

13. Interpolation. About [latex]60^\circ \text{ F}[/latex].

15. C

17. B

19.

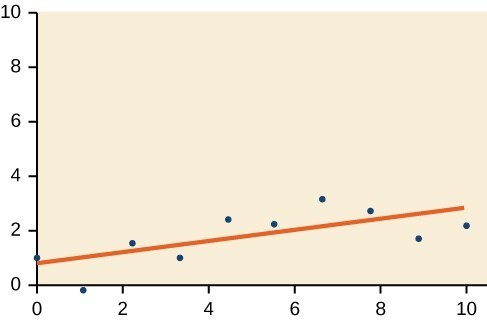
21.

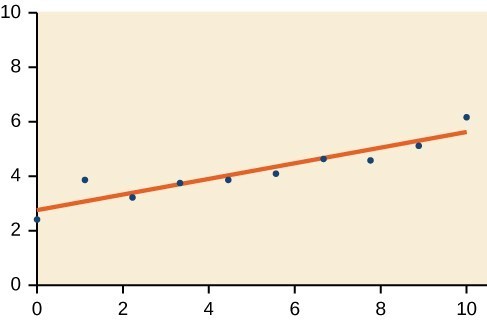
23. Yes, trend appears linear because [latex]r=0.\text{985}[/latex] and will exceed 12,000 near midyear, 2016, 24.6 years since 1992.

25. [latex]y=\text{1}.\text{64}0x+\text{13}.\text{8}00[/latex] , [latex]r=0.\text{987}[/latex]

27. [latex]y=-0.962x+26.86, r=-0.965[/latex]

29. [latex]y=-\text{1}.\text{981}x+\text{6}0.\text{197}[/latex] ; [latex]r=-0.\text{998}[/latex]

31. [latex]y=0.\text{121}x - 38.841,r=0.998[/latex]

33. [latex]\left(-2,\text{ }-6\right),\left(1,\text{ }-12\right),\left(5,\text{ }-20\right),\left(6,\text{ }-22\right),\left(9,\text{ }-28\right)[/latex]; [latex]y=-2x - 10[/latex]

35. [latex]\left(\text{189}.\text{8},0\right)[/latex] If 18,980 units are sold, the company will have a profit of zero dollars.

37. [latex]y=0.00587x+\text{1985}.4\text{1}[/latex]

39. [latex]y=\text{2}0.\text{25}x-\text{671}.\text{5}[/latex]

41. [latex]y=-\text{1}0.\text{75}x+\text{742}.\text{5}0[/latex]

43. Yes

45. Increasing

47. [latex]y=-\text{3}x+\text{26}[/latex]

49. 3

51. [latex]y=\text{2}x-\text{2}[/latex]

53. Not linear

55. parallel

57. [latex]\left(-9,0\right);\left(0,-7\right)[/latex]

59. Line 1: [latex]m=-2[/latex]; Line 2: [latex]m=-2[/latex]; Parallel

61. [latex]y=-0.2x+21[/latex]

63.

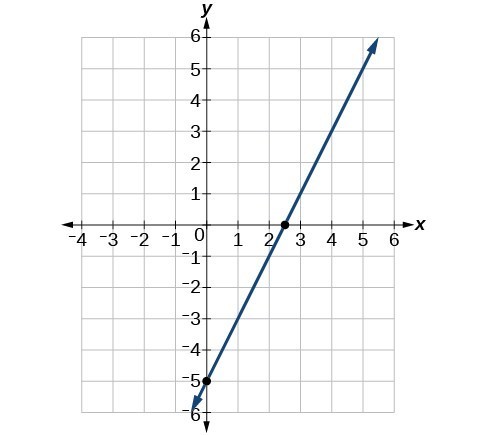
65. 250

67. 118,000

69. [latex]y=-\text{3}00x+\text{11},\text{5}00[/latex]

71. a) 800 b) 100 students per year c) [latex]P\left(t\right)=100t+1700[/latex]

73. 18,500

75. $91,625

77. Extrapolation.

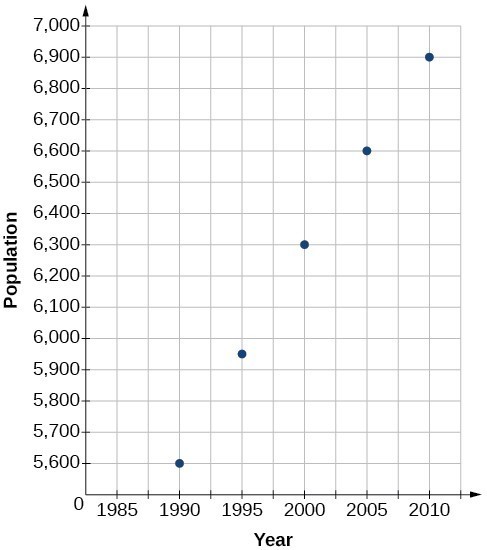
79.

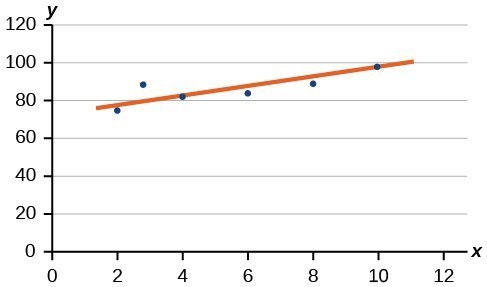
81. Midway through 2024

83. [latex]y=-1.294x+49.412;\text{ } r=-0.974[/latex]

85. Early in 2022

87. 7,660

Absolute Value Functions

1. Isolate the absolute value term so that the equation is of the form [latex]|A|=B[/latex]. Form one equation by setting the expression inside the absolute value symbol, [latex]A[/latex], equal to the expression on the other side of the equation, [latex]B[/latex]. Form a second equation by setting [latex]A[/latex] equal to the opposite of the expression on the other side of the equation, -B. Solve each equation for the variable.

3. The graph of the absolute value function does not cross the [latex]x[/latex] -axis, so the graph is either completely above or completely below the [latex]x[/latex] -axis.

5. First determine the boundary points by finding the solution(s) of the equation. Use the boundary points to form possible solution intervals. Choose a test value in each interval to determine which values satisfy the inequality.

7. [latex]|x+4|=\frac{1}{2}[/latex]

9. [latex]|f\left(x\right)-8|<0.03[/latex]</span>

11. [latex]\left\{1,11\right\}[/latex]

13. [latex]\left\{\frac{9}{4},\frac{13}{4}\right\}[/latex]

15. [latex]\left\{\frac{10}{3},\frac{20}{3}\right\}[/latex]

17. [latex]\left\{\frac{11}{5},\frac{29}{5}\right\}[/latex]

19. [latex]\left\{\frac{5}{2},\frac{7}{2}\right\}[/latex]

21. No solution

23. [latex]\left\{-57,27\right\}[/latex]

25. [latex]\left(0,-8\right);\left(-6,0\right),\left(4,0\right)[/latex]

27. [latex]\left(0,-7\right)[/latex]; no [latex]x[/latex] -intercepts

29. [latex]\left(-\infty ,-8\right)\cup \left(12,\infty \right)[/latex]

31. [latex]\frac{-4}{3}\le x\le 4[/latex]

33. [latex]\left(-\infty ,-\frac{8}{3}\right]\cup \left[6,\infty \right)[/latex]

35. [latex]\left(-\infty ,-\frac{8}{3}\right]\cup \left[16,\infty \right)[/latex]

37.

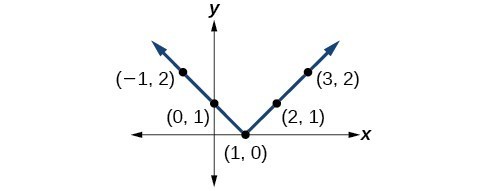
39.

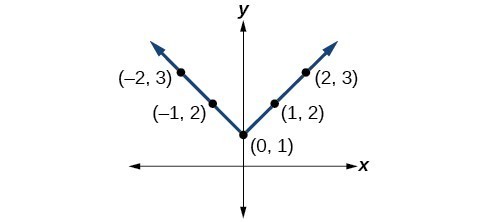
41.

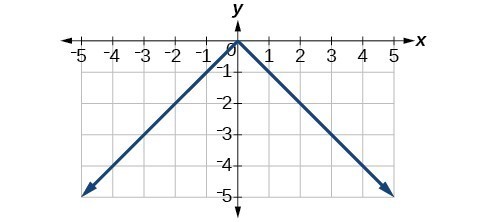
43.

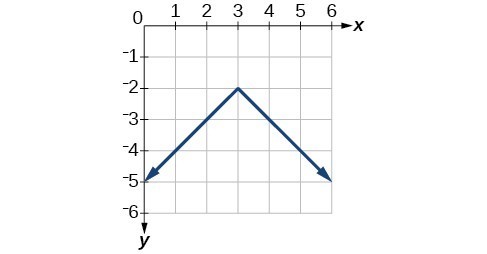
45.

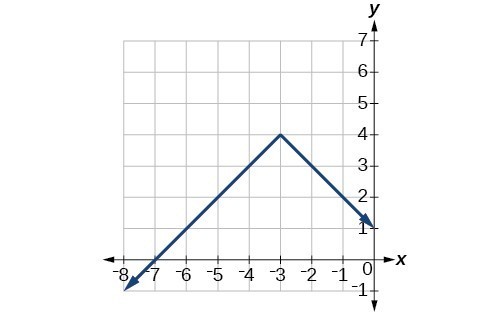
47.

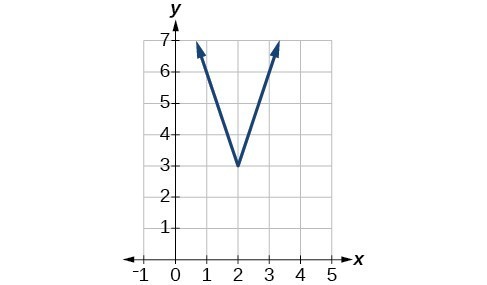
49.

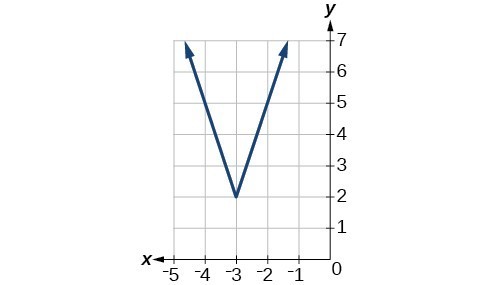
51.

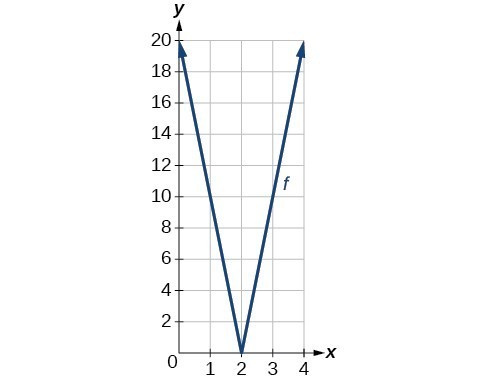
53. range: [latex]\left[0,20\right][/latex]

55. [latex]x\text{-}[/latex] intercepts:

57. [latex]\left(-\infty ,\infty \right)[/latex]

59. There is no solution for [latex]a[/latex] that will keep the function from having a [latex]y[/latex] -intercept. The absolute value function always crosses the [latex]y[/latex] -intercept when [latex]x=0[/latex].

61. [latex]|p - 0.08|\le 0.015[/latex]

63. [latex]|x - 5.0|\le 0.01[/latex]