Functions and Function Notation
1. A relation is a set of ordered pairs. A function is a special kind of relation in which no two ordered pairs have the same first coordinate.
3. When a vertical line intersects the graph of a relation more than once, that indicates that for that input there is more than one output. At any particular input value, there can be only one output if the relation is to be a function.
5. When a horizontal line intersects the graph of a function more than once, that indicates that for that output there is more than one input. A function is one-to-one if each output corresponds to only one input.
7. function
10. function
19. function
25. not a function
27. [latex]f\left(-3\right)=-11\\ f\left(2\right)=-1\\ f\left(-a\right)=-2a - 5\\-f\left(a\right)=-2a+5\\f\left(a+h\right)=2a+2h - 5[/latex]
33. [latex]\frac{g\left(x\right)-g\left(a\right)}{x-a}=x+a+2,x\ne a[/latex]
35. a. [latex]f\left(-2\right)=14[/latex]; b. [latex]x=3[/latex]
37. a. [latex]f\left(5\right)=10[/latex]; b. [latex]x=-1\text{ }[/latex] or [latex]\text{ }x=4[/latex]
39. a. [latex]f\left(t\right)=6-\frac{2}{3}t[/latex]; b. [latex]f\left(-3\right)=8[/latex]; c. [latex]t=6[/latex]
66. [latex]f\left(3\right)=53[/latex]
67. [latex]f\left(x\right)=1,x=2[/latex]
69. [latex]f\left(-2\right)=14\\ f\left(-1\right)=11\\ f\left(0\right)=8\\f\left(1\right)=5\\ f\left(2\right)=2[/latex]
89. a. [latex]g\left(5000\right)=50[/latex]; b. The number of cubic yards of dirt required for a garden of 100 square feet is 1.
91. a. The height of a rocket above ground after 1 second is 200 ft. b. the height of a rocket above ground after 2 seconds is 350 ft.
Domain and Range
1. The domain of a function depends upon what values of the independent variable make the function undefined or imaginary.
3. There is no restriction on [latex]x[/latex] for [latex]f\left(x\right)=\sqrt[3]{x}[/latex] because you can take the cube root of any real number. So the domain is all real numbers, [latex]\left(-\infty ,\infty \right)[/latex]. When dealing with the set of real numbers, you cannot take the square root of negative numbers. So [latex]x[/latex] -values are restricted for [latex]f\left(x\right)=\sqrt[]{x}[/latex] to nonnegative numbers and the domain is [latex]\left[0,\infty \right)[/latex].
4. Use parentheses for endpoints not included; use brackets for endpoints included.
8. [latex][2, \infty)[/latex].
9. [latex]\left(-\infty ,3\right][/latex]
14. [latex](-\infty,6)\cup(6,\infty)[/latex]
16. [latex][-4,4)\cup(4,\infty)[/latex]
20. [latex](3,\infty)[/latex]
22. [latex][6,\infty)[/latex]
27. Domain: [latex]\left(2,8\right][/latex] Range [latex]\left[6,8\right)[/latex]
29. Domain: [latex]\left[-4, 4\right][/latex] Range: [latex]\left[0, 2\right][/latex]
33. Domain: [latex]\left(-\infty ,1\right][/latex] Range: [latex]\left[0,\infty \right)[/latex]
39. Domain: [latex]\left(-\infty ,\infty \right)[/latex]
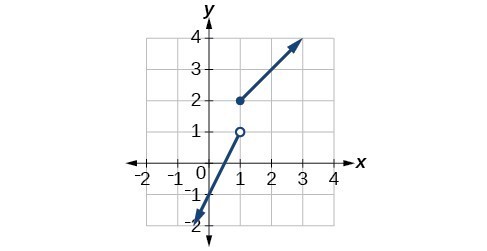
41. Domain: [latex]\left(-\infty ,\infty \right)[/latex]
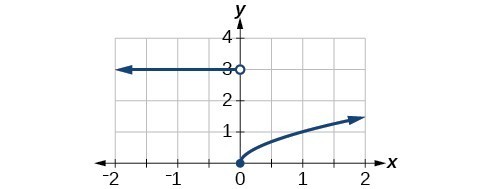
45. Domain: [latex]\left(-\infty ,\infty \right)[/latex]
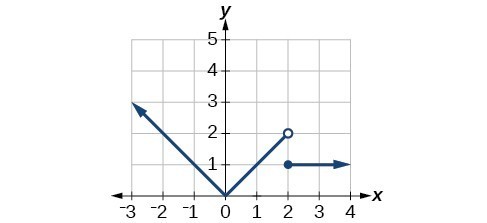
47. [latex]\begin{cases}f\left(-3\right)=1;& f\left(-2\right)=0;& f\left(-1\right)=0;& f\left(0\right)=0\end{cases}[/latex]
49. [latex]\begin{cases}f\left(-1\right)=-4;& f\left(0\right)=6;& f\left(2\right)=20;& f\left(4\right)=34\end{cases}[/latex]
Rates of Change and Behavior of Graphs
2. Increasing then decreasing implies a local maximum at [latex]x=b[/latex].
3. Absolute extrema are the highest/lowest values on the entire domain; local extrema are highest/lowest values in a neighborhood.
For exercises 5–15, find the average rate of change of each function on the interval specified for real numbers [latex]b[/latex] or [latex]h[/latex].
5. 4(b + 1)
7. 3
15. 4x+2h-3
16. [latex]-\frac{1}{3}[/latex]
17. [latex]\frac{4}{3}[/latex]
22. The function is increasing on approximately (-5, -3) and (3, 5). The function is decreasing on approximately (-3, 3).
23. The graph has a local maximum at approximately (-3, 55) and a local minimum at approximately (3, -55).
44. [latex]\frac{22125-21395}{13.5}=\frac{730}{13.5}\approx 54.1\text{ mph}[/latex]