Skip to content
Sequences and Series: Get Stronger Answer Key
Sequences and Their Notations
- First four terms: [latex]-8, -\frac{16}{5}, -4, -\frac{16}{5}[/latex]
- First four terms: [latex]2, \frac{1}{2}, \frac{8}{27}, \frac{1}{4}[/latex]
- First four terms: [latex]1.25, -5, 20, -80[/latex]
- First four terms: [latex]\frac{1}{3}, \frac{4}{5}, \frac{9}{7}, \frac{16}{9}[/latex]
- First four terms: [latex]-\frac{4}{5}, 4, -20, 100[/latex]
- [latex]\frac{1}{3}, \frac{4}{5}, \frac{9}{7}, \frac{16}{9}, \frac{25}{11}, 31, 44, 59[/latex]
- [latex]-0.6, -15, -20, -375, -80, -9375, -320[/latex]
- [latex]a_n = n^2 + 3[/latex]
- [latex]a_n = \frac{2^n}{2n}[/latex] or [latex]2^{n-1}/n[/latex]
- [latex]a_n = (-\frac{1}{2})^{n-1}[/latex]
- First five terms: [latex]3, -9, 27, -81, 243[/latex]
- First five terms: [latex]-1, 1, -9, \frac{27}{11}, \frac{891}{5}[/latex]
- [latex]\frac{1}{24}, 1, \frac{3}{4}, \frac{9}{2}, \frac{81}{4}, \frac{531,441}{8}, \frac{16}{16}[/latex]
- [latex]2, 10, 12, \frac{14}{5}, \frac{5}{5}, 2, 10, 12[/latex]
- [latex]a_1 = -8, a_n = a_{n-1} + n[/latex]
- [latex]a_1 = 35, a_n = a_{n-1} + 3[/latex]
- [latex]720[/latex]
- [latex]665,280[/latex]
- First four terms: [latex]1, \frac{1}{2}, \frac{2}{3}, \frac{3}{2}[/latex]
- First four terms: [latex]-1, 2, \frac{5}{6}, \frac{24}{11}[/latex]
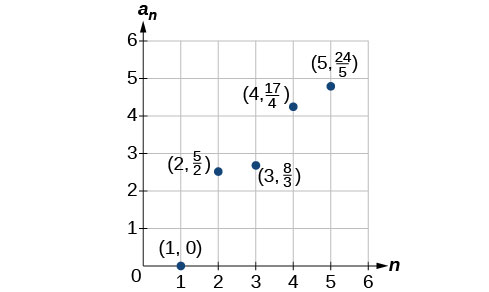

- [latex]a_n = 2^{n-2}[/latex]
- [latex]a_1 = 6, a_n = 2a_{n-1} - 5[/latex]
Arithmetic Sequences
- The common difference is [latex]\frac{1}{3}[/latex]
- The sequence is not arithmetic because [latex]16 - 4 \neq 64 - 16[/latex]
- [latex]0, \frac{2}{3}, \frac{4}{3}, 2, \frac{8}{3}[/latex]
- [latex]0, -5, -10, -15, -20[/latex]
- [latex]a_4 = 19[/latex]
- [latex]a_6 = 41[/latex]
- [latex]a_1 = 2[/latex]
- [latex]a_1 = 5[/latex]
- [latex]a_1 = 6[/latex]
- [latex]a_{21} = -13.5[/latex]
- [latex]-19, -20.4, -21.8, -23.2, -24.6[/latex]
- [latex]a_1 = 17; a_n = a_{n-1} + 9 \quad n \geq 2[/latex]
- [latex]a_1 = 12; a_n = a_{n-1} + 5 \quad n \geq 2[/latex]
- [latex]a_1 = 8.9; a_n = a_{n-1} + 1.4 \quad n \geq 2[/latex]
- [latex]a_1 = \frac{1}{5}; a_n = a_{n-1} + \frac{1}{4} \quad n \geq 2[/latex]
- [latex]1 = \frac{1}{6}; a_n = a_{n-1} - \frac{13}{12} \quad n \geq 2[/latex]
- [latex]a_1 = 4; a_n = a_{n-1} + 7; a_{14} = 95[/latex]
- First five terms: [latex]20, 16, 12, 8, 4[/latex]
- [latex]a_n = 1 + 2n[/latex]
- [latex]a_n = -105 + 100n[/latex]
- [latex]a_n = 1.8n[/latex]
- [latex]a_n = 13.1 + 2.7n[/latex]
- [latex]a_n = \frac{1}{3}n - \frac{1}{3}[/latex]
- There are [latex]10[/latex] terms in the sequence.
- There are [latex]6[/latex] terms in the sequence.
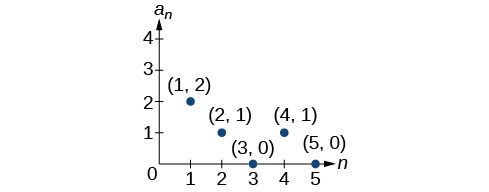
- The graph does not represent an arithmetic sequence.

Geometric Sequences
- The common ratio is [latex]-2[/latex]
- The sequence is geometric. The common ratio is [latex]2[/latex]
- The sequence is geometric. The common ratio is [latex]-\frac{1}{2}[/latex]
- The sequence is geometric. The common ratio is [latex]5[/latex]
- [latex]5, 1, \frac{1}{5}, \frac{1}{25}, \frac{1}{125}[/latex]
- [latex]800, 400, 200, 100, 50[/latex]
- [latex]a_4 = -\frac{16}{27}[/latex]
- [latex]a_7 = -\frac{9}{720}[/latex]
- [latex]7, 1.4, 0.28, 0.056, 0.0112[/latex]
- [latex]a_1 = -32, a_n = \frac{1}{2}a_{n-1}[/latex]
- [latex]a_1 = 10, a_n = -0.3a_{n-1}[/latex]
- [latex]a_1 = \frac{3}{5}, a_n = \frac{1}{6}a_{n-1}[/latex]
- [latex]a_1 = \frac{1}{512}, a_n = -4a_{n-1}[/latex]
- [latex]12, -6, 3, -\frac{3}{2}, \frac{3}{4}[/latex]
- [latex]a_n = 3^{n-1}[/latex]
- [latex]a_n = 0.8 \cdot (-5)^{n-1}[/latex]
- [latex]a_n = -(\frac{4}{5})^{n-1}[/latex]
- [latex]a_n = 3 \cdot (-\frac{1}{3})^{n-1}[/latex]
- [latex]a_{12} = \frac{1}{177,147}[/latex]
- There are [latex]12[/latex] terms in the sequence.
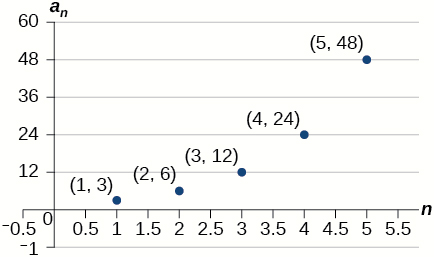
- The graph does not represent a geometric sequence.
Series and Their Notations
- [latex]\sum_{n=0}^{4} 5n[/latex]
- [latex]\sum_{k=1}^{5} 4[/latex]
- [latex]\sum_{k=1}^{20} 8k + 2[/latex]
- [latex]S_5 = \frac{5(\frac{3}{2}+\frac{7}{2})}{2}[/latex]
- [latex]S_{13} = \frac{13(3.2+5.6)}{2}[/latex]
- [latex]\sum_{k=1}^{7} 8 \cdot 0.5^{k-1}[/latex]
- [latex]S_5 = \frac{9(1-(\frac{1}{3})^5)}{1-\frac{1}{3}} = \frac{121}{9} \approx 13.44[/latex]
- [latex]S_{11} = \frac{64(1-0.2^{11})}{1-0.2} = \frac{781,249,984}{9,765,625} \approx 80[/latex]
- The series is defined. [latex]S = \frac{2}{1-0.8}[/latex]
- The series is defined. [latex]S = \frac{-1}{1-(-\frac{1}{2})}[/latex]
- [latex]49[/latex]
- [latex]254[/latex]
- [latex]S_7 = \frac{147}{2}[/latex]
- [latex]S_{11} = \frac{55}{2}[/latex]
- [latex]S_7 = 5208.4[/latex]
- [latex]S_{10} = -\frac{1023}{256}[/latex]
- [latex]S = -\frac{4}{3}[/latex]
- [latex]S = 9.2[/latex]
- [latex]$3,705.42[/latex]
- [latex]$695,823.97[/latex]
- [latex]420[/latex] feet
- [latex]12[/latex] feet




