Skip to content
Linear Equations and Inequalities: Get Stronger Answer Key
Graphing and Analyzing Linear Equations
- The x-intercept is [latex](2, 0)[/latex] and the y-intercept is [latex](0, 6)[/latex].
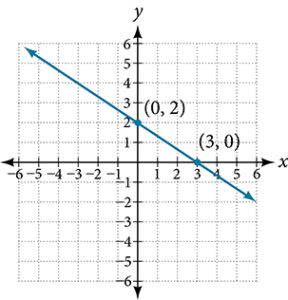
- The x-intercept is [latex](2, 0)[/latex] and the y-intercept is [latex](0, -3)[/latex].
- The x-intercept is [latex](3, 0)[/latex] and the y-intercept is [latex](0, \frac{9}{8})[/latex].
- [latex]y = 4 - 2x[/latex]
- [latex]y = \frac{5 - 2x}{3}[/latex]
- [latex]y = 2x - \frac{4}{5}[/latex]
- [latex]d = \sqrt{74}[/latex]
- [latex]d = \sqrt{36} = 6[/latex]
- [latex]d \approx 62.97[/latex]
- [latex]\left( 3, -\frac{3}{2} \right)[/latex]
- [latex]\left( 2, -1 \right)[/latex]
- [latex](0, 0)[/latex]
- [latex]y = 0[/latex]
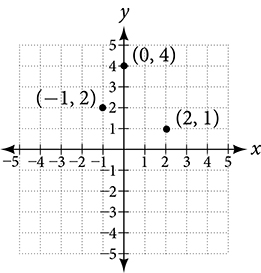 not collinear
not collinear- [latex]A: (-3, 2), B: (1, 3), C: (4, 0)[/latex]
-
| [latex]x[/latex] |
[latex]y[/latex] |
| [latex]-3[/latex] |
[latex]1[/latex] |
| [latex]0[/latex] |
[latex]2[/latex] |
| [latex]3[/latex] |
[latex]3[/latex] |
| [latex]6[/latex] |
[latex]4[/latex] |
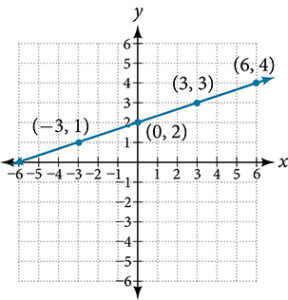
-
| [latex]x[/latex] |
[latex]y[/latex] |
| [latex]-3[/latex] |
[latex]0[/latex] |
| [latex]0[/latex] |
[latex]1.5[/latex] |
| [latex]3[/latex] |
[latex]3[/latex] |
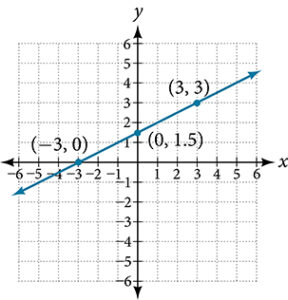
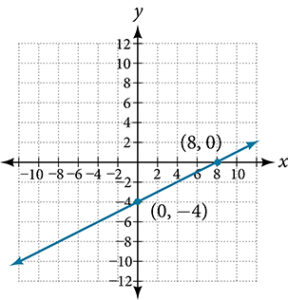
- [latex]d = 8.246[/latex]
- [latex]d = 5[/latex]
- [latex](-3, 4)[/latex]
- [latex]m = -\frac{9}{7}[/latex]
- [latex]m = \frac{3}{2}[/latex]
Equations of Lines
- [latex]x = 2[/latex]
- [latex]x = \frac{2}{7}[/latex]
- [latex]x = 6[/latex]
- [latex]x = 3[/latex]
- [latex]x = -14[/latex]
- [latex]x \neq -4; x = -3[/latex]
- [latex]x \neq 1;[/latex] when we solve this we get [latex]x = 1[/latex], which is excluded, therefore NO solution
- [latex]x \neq 0; x = -\frac{5}{2}[/latex]
- [latex]y = \frac{4}{5}x + \frac{14}{5}[/latex]
- [latex]y = \frac{3}{4}x + 2[/latex]
- [latex]y = \frac{1}{2}x + \frac{5}{2}[/latex]
- [latex]y = -3x - 5[/latex]
- [latex]y = 7[/latex]
- [latex]y = -4[/latex]
- [latex]8x + 5y = 7[/latex]
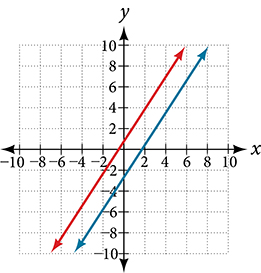 Parallel
Parallel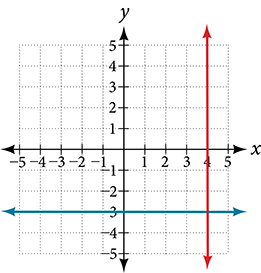 Perpendicular
Perpendicular
Modeling with Linear Equations
- [latex]2,000 - x[/latex]
- [latex]v + 10[/latex]
- [latex]\text{Ann: } 23; \text{Beth: } 46[/latex]
- [latex]20 + 0.05m[/latex]
- [latex]300[/latex] min
- [latex]90 + 40P[/latex]
- [latex]6[/latex] devices
- [latex]50,000 - x[/latex]
- [latex]4[/latex] h
- She traveled for [latex]2[/latex] hours at [latex]20[/latex]mi/h, or [latex]40[/latex] miles.
- [latex]\$5,000 \text{ at 8% and } \$15{,}000 \text{ at 12%}[/latex]
- [latex]B = 100 + 0.05x[/latex]
- Plan A
- [latex]R = 9[/latex]
- [latex]r = \frac{4}{5} \text{ or } 0.8[/latex]
- [latex]W = \frac{P - 2L}{2} = \frac{58 - 2(15)}{2} = 14[/latex]
- [latex]f = \frac{pq}{p + q} = \frac{8(13)}{8 + 13} = \frac{104}{21}[/latex]
- [latex]m = - \frac{5}{4}[/latex]
- [latex]h = \frac{2A}{b_1 + b_2}[/latex]
- [latex]\text{length} = 360 \, \text{ft}; \, \text{width} = 160 \, \text{ft}[/latex]
- [latex]405 \, \text{mi}[/latex]
- [latex]28.7[/latex]
- [latex]h = \frac{V}{\pi r^2}[/latex]
- [latex]r = \sqrt{\frac{V}{\pi h}}[/latex]
- [latex]C = 12\pi[/latex]
Linear Inequalities
- [latex]14 + 7i[/latex]
- [latex]-\frac{23}{29} + \frac{15}{29}i[/latex]
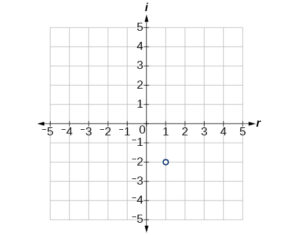
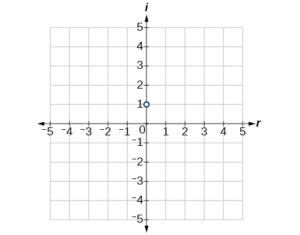
- [latex]2 - \frac{2}{3}i[/latex]
- [latex]4 - 6i[/latex]
- [latex]128i[/latex]
- [latex]\left( \frac{\sqrt{3}}{2} + \frac{1}{2}i \right)^6 = -1[/latex]
- [latex]3i[/latex]
- [latex]0[/latex]
- [latex]5 - 5i[/latex]
- [latex]-2i[/latex]
 not collinear
not collinear



 Parallel
Parallel Perpendicular
Perpendicular
