- Calculate square roots and apply them in basic operations like addition, subtraction, and rationalizing the denominators.
- Use the product and quotient rules to simplify expressions that include square roots.
- Understand how to use rational exponents in expressions and recognize their connection to roots for simplifying calculations.
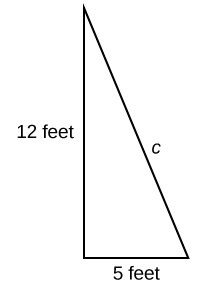
A hardware store sells [latex]16[/latex]-ft ladders and [latex]24[/latex]-ft ladders. A window is located [latex]12[/latex] feet above the ground. A ladder needs to be purchased that will reach the window from a point on the ground [latex]5[/latex] feet from the building. To find out the length of ladder needed, we can draw a right triangle as shown, and use the Pythagorean Theorem.
[latex]\begin{align} {a}^{2}+{b}^{2}& = {c}^{2} \\ {5}^{2}+{12}^{2}& = {c}^{2} \\ 169& = {c}^{2} \end{align}[/latex]
Now we need to find out the length that, when squared, is [latex]169,[/latex] to determine which ladder to choose. In other word we need to find a square root. In this section we will investigate methods of finding solutions to problems such as this one.
Square Roots
When the square root of a number is squared, the result is the original number. Since [latex]{4}^{2}=16[/latex], the square root of [latex]16[/latex] is [latex]4[/latex]. The square root function is the inverse of the squaring function just as subtraction is the inverse of addition. To undo squaring, we take the square root.
Square Root
The square root of a number [latex]a[/latex] refers to any number [latex]x[/latex] such that [latex]x^2 = a[/latex].
For positive number [latex]a[/latex], there are always two square roots: one positive and one negative.
When we talk about square roots in math, we usually mean both the positive and negative numbers that, when multiplied by themselves, give us the original number. In math classes, especially when you’re solving problems or learning algebra, it’s important to think about both these answers unless we’re told to find just one. This helps us understand all the possible solutions to an equation, which is a big part of learning how to solve math problems correctly.
As we explore square roots further, there’s a special version we often use called the principal square root. This refers specifically to the positive square root of a number. It’s helpful to know about this because it’s commonly used in many situations.
principal square root
The principal square root of [latex]a[/latex] is the nonnegative number that when multiplied by itself equals [latex]a[/latex].
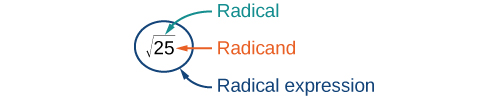
The principal square root of [latex]a[/latex] is written as [latex]\sqrt{a}[/latex]. The symbol is called a radical, the term under the symbol is called the radicand, and the entire expression is called a radical expression.
The square root obtained using a calculator is the principal square root.
- [latex]\sqrt{100}[/latex]
- [latex]\sqrt{\sqrt{16}}[/latex]
- [latex]\sqrt{25+144}[/latex]
- [latex]\sqrt{49}-\sqrt{81}[/latex]
Question! For [latex]\sqrt{25+144}[/latex], can we find the square roots before adding?