Quadratic Functions: Learn It 5

Lumen Learning

Quadratic Functions: Learn It 5

Transformations of Quadratic Functions General form

Often times when given quadratic functions they will be in the general form, [latex]f(x)=ax^2+bx+c[/latex] where [latex]a \ne 0[/latex].

How Changing [latex]a[/latex] Impacts the Graph of a Parabola

Changing [latex]a[/latex] affects the width of the parabola and whether it opens up ([latex]a>0[/latex]) or down ([latex]a<0[/latex]).

changing [latex]a[/latex] of a parabola

Changing [latex]a[/latex] changes the width of the parabola.

Width of the parabola:
- When [latex]|a| > 1[/latex], the parabola becomes narrower (steeper)
- When [latex]0 < |a| < 1[/latex], the parabola becomes wider (flatter)
- The larger the absolute value of [latex]a[/latex], the narrower the parabola
Direction of opening:
- If a [latex]> 0[/latex], the parabola opens upward (U-shaped)
- If [latex]a < 0[/latex], the parabola opens downward (inverted U-shape)
Stretching and compressing:
- Multiplying ‘[latex]a[/latex]‘ by a factor stretches the graph vertically by that factor
- Dividing ‘[latex]a[/latex]‘ by a factor compresses the graph vertically by that factor

In the following example, we show how changing the value of [latex]a[/latex] will affect the graph of the function.

Match each function with its graph.

[latex]\displaystyle f(x)=3{{x}^{2}}[/latex]
[latex]\displaystyle f(x)=-3{{x}^{2}}[/latex]
[latex]\displaystyle f(x)=\frac{1}{2}{{x}^{2}}[/latex]

How Changing [latex]c[/latex] Impacts the Graph of a Parabola

Changing [latex]c[/latex] affects the vertical position of the entire parabola.

changing [latex]c[/latex] of a parabola

Changing [latex]c[/latex] moves the parabola up or down so that the [latex]y[/latex] intercept is ([latex]0, c[/latex]).

[latex]c[/latex] represents the [latex]y[/latex]-intercept of the parabola
Positive [latex]c[/latex] shifts the parabola up
Negative c shifts the parabola down
The magnitude of c determines the amount of vertical shift

In the next example, we show how changes to [latex]c[/latex] affect the graph of the function.

Match each of the following functions with its graph.

[latex]\displaystyle f(x)={{x}^{2}}+3[/latex]
[latex]\displaystyle f(x)={{x}^{2}}-3[/latex]

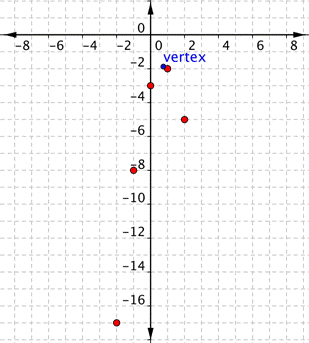
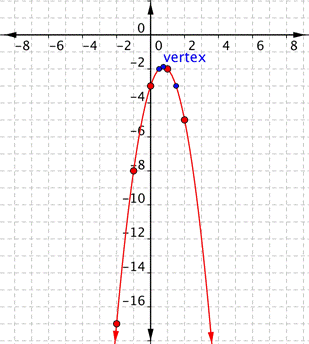
How Changing [latex]b[/latex] Impacts the Graph of a Parabola

Changing [latex]b[/latex] moves the line of reflection, which is the vertical line that passes through the vertex ( the high or low point) of the parabola. It may help to know how to calculate the vertex of a parabola to understand how changing the value of [latex]b[/latex] in a function will change its graph.

changing [latex]b[/latex] of a parabola

Changing [latex]b[/latex] affects the horizontal position of the vertex and the axis of symmetry of the parabola.

Axis of symmetry:
- The axis of symmetry is given by [latex]x=\dfrac{-b}{2a}[/latex]
- Changing [latex]b[/latex] shifts this axis left or right
A positive [latex]b[/latex] shifts the vertex left of the y-axis
A negative [latex]b[/latex] shifts the vertex right of the y-axis
The larger the absolute value of [latex]b[/latex], the greater the shift

To find the vertex of the parabola, use the formula [latex]\displaystyle \left( \frac{-b}{2a},f\left( \frac{-b}{2a} \right) \right)[/latex].For example, if the function being considered is [latex]f(x)=2x^2-3x+4[/latex], to find the vertex, first calculate [latex]\Large\frac{-b}{2a}[/latex][latex]a = 2[/latex], and [latex]b = -3[/latex], therefore [latex]\dfrac{-b}{2a}=\dfrac{-(-3)}{2(2)}=\dfrac{3}{4}[/latex].This is the [latex]x[/latex] value of the vertex.

Now evaluate the function at [latex]x =\Large\frac{3}{4}[/latex] to get the corresponding y-value for the vertex.

[latex]f\left( \dfrac{-b}{2a} \right)=2\left(\dfrac{3}{4}\right)^2-3\left(\dfrac{3}{4}\right)+4=2\left(\dfrac{9}{16}\right)-\dfrac{9}{4}+4=\dfrac{18}{16}-\dfrac{9}{4}+4=\dfrac{9}{8}-\dfrac{9}{4}+4=\dfrac{9}{8}-\dfrac{18}{8}+\dfrac{32}{8}=\dfrac{23}{8}[/latex].

The vertex is at the point [latex]\left(\dfrac{3}{4},\dfrac{23}{8}\right)[/latex]. This means that the vertical line of reflection passes through this point as well.

It is not easy to tell how changing the values for [latex]b[/latex] will change the graph of a quadratic function, but if you find the vertex, you can tell how the graph will change.

In the next example, we show how changing [latex]b[/latex] can change the graph of the quadratic function.

Match each of the following functions with its graph.

[latex]\displaystyle f(x)={{x}^{2}}+2x[/latex]
[latex]\displaystyle f(x)={{x}^{2}}-2x[/latex]

Note that the vertex can change if the value for [latex]c[/latex] changes because the [latex]y[/latex]-value of the vertex is calculated by substituting the [latex]x[/latex]-value into the function.

Graph [latex]f(x)=−2x^{2}+3x–3[/latex].

Before making a table of values, look at the values of [latex]a[/latex] and [latex]c[/latex] to get a general idea of what the graph should look like.

[latex]a=−2[/latex], so the graph will open down and be thinner than [latex]f(x)=x^{2}[/latex].

[latex]c=−3[/latex], so it will move to intersect the [latex]y[/latex]-axis at [latex](0,−3)[/latex].

To find the vertex of the parabola, use the formula [latex]\displaystyle \left( \dfrac{-b}{2a},f\left( \dfrac{-b}{2a} \right) \right)[/latex]. Finding the vertex may make graphing the parabola easier.

[latex]\text{Vertex }\text{formula}=\left( \dfrac{-b}{2a},f\left( \dfrac{-b}{2a} \right) \right)[/latex]

[latex]x[/latex]-coordinate of vertex:

[latex]\displaystyle \dfrac{-b}{2a}=\dfrac{-(3)}{2(-2)}=\dfrac{-3}{-4}=\dfrac{3}{4}[/latex]

[latex]y[/latex]-coordinate of vertex:

[latex]\displaystyle \begin{array}{l}f\left( \dfrac{-b}{2a} \right)=f\left( \dfrac{3}{4} \right)\\\,\,\,f\left( \dfrac{3}{4} \right)=-2{{\left( \dfrac{3}{4} \right)}^{2}}+3\left( \dfrac{3}{4} \right)-3\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=-2\left( \dfrac{9}{16} \right)+\dfrac{9}{4}-3\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\dfrac{-18}{16}+\dfrac{9}{4}-3\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\dfrac{-9}{8}+\dfrac{18}{8}-\dfrac{24}{8}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=-\dfrac{15}{8}\end{array}[/latex]

Vertex: [latex]\displaystyle \left( \dfrac{3}{4},-\dfrac{15}{8} \right)[/latex]

Use the vertex, [latex]\displaystyle \left( \dfrac{3}{4},-\dfrac{15}{8} \right)[/latex], and the properties you described to get a general idea of the shape of the graph. You can create a table of values to verify your graph. Notice that in this table, the [latex]x[/latex] values increase. The [latex]y[/latex] values increase and then start to decrease again. This indicates a parabola.

[latex]x[/latex]	[latex]f(x)[/latex]
[latex]−2[/latex]	[latex]−17[/latex]
[latex]−1[/latex]	[latex]−8[/latex]
[latex]0[/latex]	[latex]−3[/latex]
[latex]1[/latex]	[latex]−2[/latex]
[latex]2[/latex]	[latex]−5[/latex]

Vertex at negative three-fourths, negative 15-eighths. Other points are plotted: the point negative 2, negative 17; the point negative 1, negative 8; the point 0, negative 3; the point 1, negative 2; and the point 2, negative 5.

Connect the points as best you can using a smooth curve. Remember that the parabola is two mirror images, so if your points do not have pairs with the same value, you may want to include additional points (such as the ones in blue shown below). Plot points on either side of the vertex.

[latex]x=\Large\frac{1}{2}[/latex] and [latex]x=\Large\frac{3}{2}[/latex] are good values to include.

A parabola drawn through the points in the previous graph