Graphing Linear Functions Cont.

Graphing a Linear Function Using Transformations

Another option for graphing is to use transformations on the identity function [latex]f\left(x\right)=x[/latex]. A function may be transformed by a shift up, down, left, or right. A function may also be transformed using a reflection, stretch, or compression.

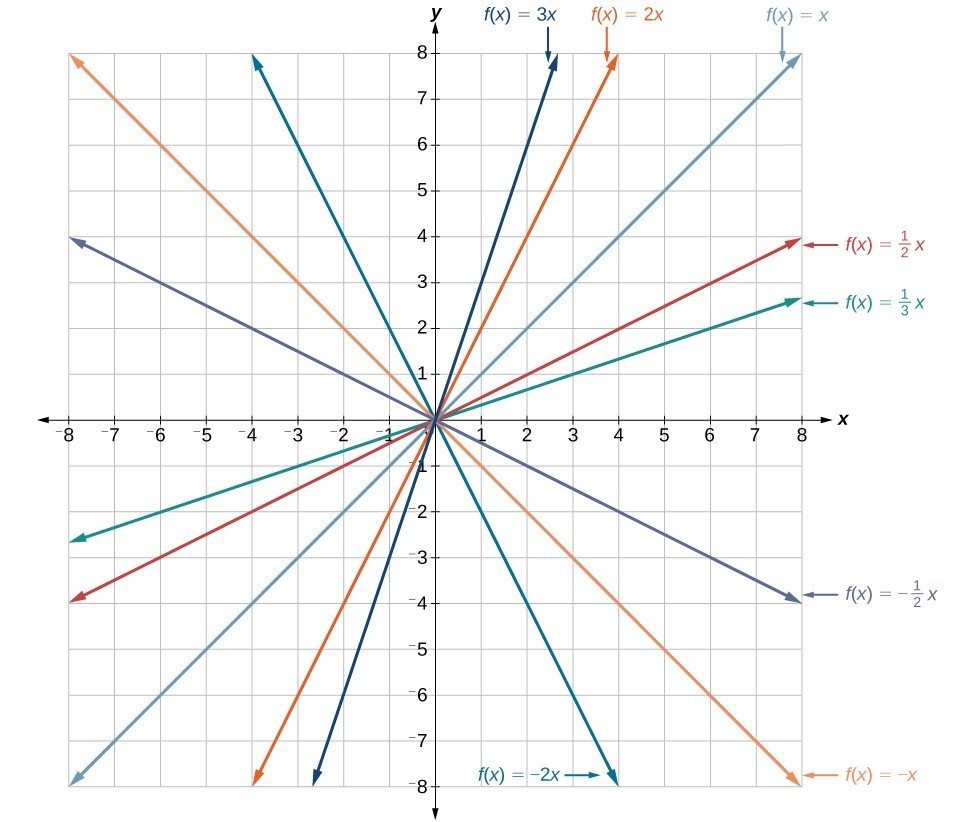
Vertical Stretch or Compression

In the equation [latex]f\left(x\right)=mx[/latex], the [latex]m[/latex] is acting as the vertical stretch or compression of the identity function. When [latex]m[/latex] is negative, there is also a vertical reflection of the graph. Notice that multiplying the equation [latex]f\left(x\right)=x[/latex] by [latex]m[/latex] stretches the graph of [latex]f[/latex] by a factor of [latex]m[/latex] units if [latex]m > 1[/latex] and compresses the graph of [latex]f[/latex] by a factor of [latex]m[/latex] units if [latex]0 < m < 1[/latex]. This means the larger the absolute value of [latex]m[/latex], the steeper the slope.

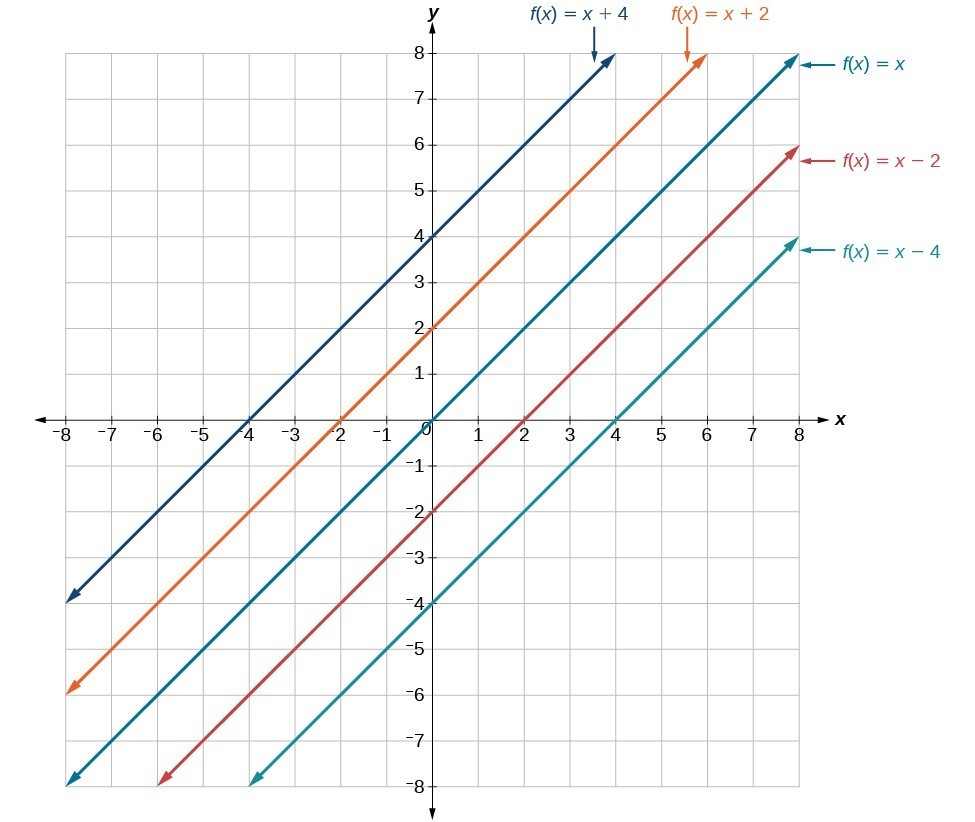
Vertical Shift

In [latex]f\left(x\right)=mx+b[/latex], the [latex]b[/latex] acts as the vertical shift, moving the graph up and down without affecting the slope of the line. Notice that adding a value of [latex]b[/latex] to the equation of [latex]f\left(x\right)=x[/latex] shifts the graph of [latex]f[/latex] a total of [latex]b[/latex] units up if [latex]b[/latex] is positive and [latex]|b|[/latex] units down if [latex]b[/latex] is negative.

 

Using vertical stretches or compressions along with vertical shifts is another way to look at identifying different types of linear functions. Although this may not be the easiest way to graph this type of function, it is still important to practice each method.

How To: Given the equation of a linear function, use transformations to graph the linear function in the form [latex]f\left(x\right)=mx+b[/latex].

1. Graph [latex]f\left(x\right)=x[/latex].
2. Vertically stretch or compress the graph by a factor [latex]m[/latex].
3. Shift the graph up or down [latex]b[/latex] units.

Graph [latex]f(x)=\frac{1}{2}x - 3[/latex] using transformations.

Show Solution

The equation for the function shows that [latex]m=\frac{1}{2}[/latex] so the identity function is vertically compressed by [latex]\frac{1}{2}[/latex]. The equation for the function also shows that [latex]b=-3[/latex], so the identity function is vertically shifted down [latex]3[/latex] units.

First, graph the identity function, and show the vertical compression.

The function [latex]y=x[/latex] compressed by a factor of [latex]\frac{1}{2}[/latex].

 

Then, show the vertical shift.

The function [latex]y=\frac{1}{2}x[/latex] shifted down 3 units.

Q & A In the example above, could we have sketched the graph by reversing the order of the transformations? No. The order of the transformations follows the order of operations. When the function is evaluated at a given input, the corresponding output is calculated by following the order of operations. This is why we performed the compression first. For example, following order of operations, let the input be 2.

[latex]\begin{array}{l}f\text{(2)}=\frac{\text{1}}{\text{2}}\text{(2)}-\text{3}\hfill \\ =\text{1}-\text{3}\hfill \\ =-\text{2}\hfill \end{array}[/latex]