Building Linear Models
In the real world, problems are not always explicitly stated in terms of a function or represented with a graph. Fortunately, we can analyze the problem by first representing it as a linear function and then interpreting the components of the function. As long as we know, or can figure out, the initial value and the rate of change of a linear function, we can solve many different kinds of real-world problems.
This process of translating real-world problems into mathematical terms and solving them is known as modeling. When modeling scenarios with linear functions and solving problems involving quantities with a constant rate of change, we can use the following problem solving strategy:
- Identify changing quantities, and then define descriptive variables to represent those quantities. When appropriate, sketch a picture or define a coordinate system.
- Look for information that provides values for the variables or values for parts of the functional model, such as slope and initial value.
- Determine what we are trying to find, identify, solve, or interpret.
- Identify a solution pathway from the provided information to what we are trying to find. Often this will involve checking and tracking units, building a table, or even finding a formula for the function being used to model the problem.
- When needed, write a formula for the function.
- Solve or evaluate the function using the formula.
- Reflect on whether your answer is reasonable for the given situation and whether it makes sense mathematically.
- Clearly convey your result using appropriate units, and answer in full sentences when necessary.
Let’s explore this through an example.
Emily is a college student who plans to spend a summer in Seattle. She has saved [latex]$3,500[/latex] for her trip and anticipates spending [latex]$400[/latex] each week on rent, food, and activities.
How can we write a linear model to represent her situation? What would be the [latex]x[/latex]-intercept, and what can she learn from it?
To answer these and related questions, we can create a model using a linear function. Models such as this one can be extremely useful for analyzing relationships and making predictions based on those relationships
In her situation, there are two changing quantities: time and money. The amount of money she has remaining while on vacation depends on how long she stays. We can use this information to define our variables, including units.
- Output: [latex]M[/latex], money remaining, in dollars
- Input: [latex]t[/latex], time, in weeks
So, the amount of money remaining depends on the number of weeks. Hence, amount of money remaining is a function of time: [latex]M(t)[/latex].
We can also identify the initial value and the rate of change.
- Initial Value: She saved [latex]$3,500[/latex], so [latex]$3,500[/latex] is the initial value for [latex]M[/latex].
- Rate of Change: She anticipates spending [latex]$400[/latex] each week, so [latex]–$400[/latex] per week is the rate of change, or slope.
Notice that the unit of dollars per week matches the unit of our output variable divided by our input variable. Also, because the slope is negative, the linear function is decreasing. This should make sense because she is spending money each week.
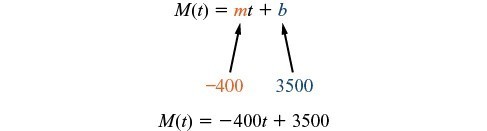
The rate of change is constant, so we can start with the linear model [latex]M(t)=mt+b[/latex]. Then we can substitute the intercept and slope provided.
To find the [latex]x[/latex]-intercept, we set the output to zero and solve for the input.
[latex]\begin{array}{l}0=-400t+3500\hfill \\ t=\frac{3500}{400}\hfill \\ t=8.75\hfill \end{array}[/latex]
The [latex]x[/latex]-intercept is [latex]8.75[/latex] weeks. Because this represents the input value when the output will be zero, we could say that Emily will have no money left after [latex]8.75[/latex] weeks.
When modeling any real-life scenario with functions, there is typically a limited domain over which that model will be valid—almost no trend continues indefinitely. Here the domain refers to the number of weeks. In this case, it doesn’t make sense to talk about input values less than zero. A negative input value could refer to a number of weeks before she saved [latex]$3,500[/latex], but the scenario discussed poses the question once she saved [latex]$3,500[/latex] because this is when her trip and subsequent spending starts. It is also likely that this model is not valid after the [latex]x[/latex]-intercept, unless Emily will use a credit card and goes into debt. The domain represents the set of input values, so the reasonable domain for this function is [latex]0\le t\le 8.75[/latex].
In the above example, we were given a written description of the situation. We followed the steps of modeling a problem to analyze the information. However, the information provided may not always be the same. Sometimes we might be provided with an intercept. Other times we might be provided with an output value. We must be careful to analyze the information we are given and use it appropriately to build a linear model.