- Use the properties of logarithms to solve exponential models for time
- Identify the carrying capacity in a logistic growth model
- Use a logistic growth model to predict growth
Reversing an Exponent
Earlier, we found that since Olympia, WA had a population of [latex]245[/latex] thousand in 2008 and had been growing at [latex]3\%[/latex] per year, the population could be modeled by the equation
[latex]P_n = (1+0.03)^{n}(245,000)[/latex], or equivalently, [latex]P_n = 245,000(1.03)^{n}[/latex].
Using this equation, we were able to predict the population in the future.
Suppose we wanted to know when the population of Olympia would reach [latex]400[/latex] thousand, rather than what the population would be after a set amount of time. Since we are looking for the year [latex]n[/latex] when the population will be [latex]400[/latex] thousand, we would need to solve the equation
[latex]400,000 = 245,000(1.03)^{n}[/latex]
Dividing both sides by [latex]245,000[/latex] gives
[latex]1.6327 = 1.03^{n}[/latex]
One approach to this problem would be to create a table of values, or to use technology to draw a graph to estimate the solution.
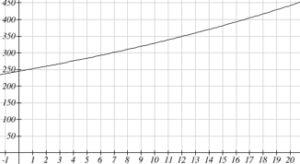
From the graph, we can estimate that the solution will be around [latex]16[/latex] to [latex]17[/latex] years after 2008 (2024 to 2025). This is pretty good, but we’d really like to have an algebraic tool to answer this question. To do that, we need to introduce a new function that will undo exponentials, similar to how a square root undoes a square. For exponentials, the function we need is called a logarithm. It is the inverse of the exponential, meaning it undoes the exponential. While there is a whole family of logarithms with different bases, we will focus on the common log, which is based on the exponential [latex]10^{n}[/latex].
common logarithm
The common logarithm, written [latex]log(x)[/latex], undoes the exponential [latex]10^{x}[/latex]
This means that [latex]log(10^{x}) = x[/latex], and likewise [latex]10^{log(x)} = x[/latex]
This also means the statement [latex]10^{a} = b[/latex] is equivalent to the statement [latex]log(b) = a[/latex]
[latex]log(x)[/latex] is read as “log of [latex]x[/latex]”, and means “the logarithm of the value [latex]x[/latex]”. It is important to note that this is not multiplication – the log doesn’t mean anything by itself, just like √ doesn’t mean anything by itself; it has to be applied to a number.
- Product Rule [latex]{a}^{m}\cdot {a}^{n}={a}^{m+n}[/latex]
- Quotient Rule [latex]\dfrac{{a}^{m}}{{a}^{n}}={a}^{m-n}[/latex]
- Power Rule [latex]{\left({a}^{m}\right)}^{n}={a}^{m\cdot n}[/latex]
- Zero Exponent [latex]{a}^{0}=1[/latex]
- Negative Exponent [latex]{a}^{-n}=\dfrac{1}{{a}^{n}} \text{ and } {a}^{n}=\dfrac{1}{{a}^{-n}}[/latex]
- Power of a Product [latex]\large{\left(ab\right)}^{n}={a}^{n}{b}^{n}[/latex]
- Power of a Quotient [latex]\large{\left(\dfrac{a}{b}\right)}^{n}=\dfrac{{a}^{n}}{{b}^{n}}[/latex]
You’ve seen that the common logarithm, written [latex]log(x)[/latex], undoes the exponential [latex]10^{x}[/latex].
This works because the common logarithm has a base of [latex]10[/latex], just like the exponential expression[latex]10^{x}[/latex]. That is, [latex]log(x)[/latex] undoes [latex]10^{x}[/latex] because [latex]log(x)[/latex] is the number we to which we raise [latex]10[/latex] to obtain the number [latex]x[/latex].
In the EXAMPLE below, part (a) asks you to evaluate [latex]log(100)[/latex].
[latex]log(100) = log(10^{2})[/latex], which gives us the statement [latex]x = 2[/latex] because [latex]2[/latex] is the number to which we raise [latex]10[/latex] to obtain [latex]100[/latex].
Part (d) asks you to evaluate [latex]log(1/100)[/latex]. First, try rewriting [latex]1/100[/latex] as the base [latex]10[/latex] raised to a number.
- [latex]log(100)[/latex]
- [latex]log(1000)[/latex]
- [latex]log(10000)[/latex]
- [latex]log(\frac{1}{100})[/latex]
- [latex]log(1)[/latex]
It is helpful to note that from the first three parts of the previous example that the number we’re taking the log of has to get [latex]10[/latex] times bigger for the log to increase in value by [latex]1[/latex].
Of course, most numbers cannot be written as a nice simple power of [latex]10[/latex]. For those numbers, we can evaluate the log using a scientific calculator with a log button.
With an equation, just like we can add a number to both sides, multiply both sides by a number, or square both sides, we can also take the logarithm of both sides of the equation and end up with an equivalent equation. This will allow us to solve some simple equations.
- Solve [latex]10^{x}= 1000[/latex]
- Solve [latex]10^{x} = 3[/latex]
- Solve [latex]2(10^{x}) = 8[/latex]
properties of logs: exponent property
To show why this is true, we offer a proof.
Since the logarithm and exponential undo each other, [latex]{{10}^{\log{A}}}=A[/latex].
So [latex]{{A}^{r}}={{\left({{10}^{\log{A}}}\right)}^{r}}[/latex]
Utilizing the exponential rule that states [latex]{{\left({{x}^{a}}\right)}^{b}}={{x}^{ab}}[/latex],
[latex]{{A}^{r}}={{\left({{10}^{\log{A}}}\right)}^{r}}={{10}^{r\log{A}}}[/latex]
So then [latex]\log\left({{A}^{r}}\right)=\log\left({{10}^{r\log{A}}}\right)[/latex]
Again utilizing the property that the log undoes the exponential on the right side yields the result
[latex]\log\left({{A}^{r}}\right)=r\log{A}[/latex]