Introduction to Real Numbers: Learn It 1

  • Categorize real numbers as counting numbers, whole numbers, rational numbers, irrational numbers, or integers
  • Recognize and use the properties of real numbers
  • Simplify and evaluate an algebraic equation

Categories of Real Numbers

Whole, Counting Numbers, and Integers

In elementary mathematics, we frequently use the most fundamental set of numbers, which we typically employ for counting objects: [latex]1, 2, 3, 4, 5, ...[/latex] and so forth. These numbers are referred to as the counting numbers. The discovery of the number zero was a big step in the history of mathematics. Including zero with the counting numbers gives a new set of numbers called the whole numbers.

Integers are counting numbers, their opposites, and zero.

 

[latex]\dots{-3,-2,-1,0,1,2,3}\dots[/latex]

whole, counting numbers, and integers

Counting numbers start with [latex]1[/latex] and continue.

 

[latex]1,2,3,4,5\dots[/latex]

 

Whole numbers are the counting numbers and zero.

 

[latex]0,1,2,3,4,5\dots[/latex]

Integers are counting numbers, their opposites, and zero.

 

[latex]\dots{-3,-2,-1,0,1,2,3}\dots[/latex]

Rational Numbers

What type of numbers would you get if you started with all the integers and then included all the fractions? The numbers you would have form the set of rational numbers. A rational number is a number that can be written as a ratio of two integers.

rational number

A rational number is a number that can be written in the form [latex]{\Large\frac{p}{q}}[/latex], where [latex]p[/latex] and [latex]q[/latex] are integers and [latex]q\ne o[/latex].

 

All fractions, both positive and negative, are rational numbers.

We can write each of the following as a rational number.

  1. [latex]7=\dfrac{7}{1}[/latex].
  2. [latex]0=\dfrac{0}{1}[/latex].
  3. [latex]-8=-\dfrac{8}{1}[/latex].

Because they are fractions, any rational number can also be expressed in decimal form. Any rational number can be represented as either:

  1. a terminating decimal: [latex]\frac{15}{8}=1.875[/latex], or
  2. a repeating decimal: [latex]\frac{4}{11}=0.36363636\dots =0.\overline{36}[/latex]

We use a line drawn over the repeating block of numbers instead of writing the group multiple times.

Are Integers Rational Numbers?To decide if an integer is a rational number, we try to write it as a ratio of two integers. An easy way to do this is to write it as a fraction with denominator one.

[latex]3=\Large\frac{3}{1}\normalsize ,\space-8=\Large\frac{-8}{1}\normalsize ,\space0=\Large\frac{0}{1}[/latex]

Since any integer can be written as the ratio of two integers, all integers are rational numbers. Remember that all the counting numbers and all the whole numbers are also integers, and so they, too, are rational.

What about decimals? Are they rational? Let’s look at a few to see if we can write each of them as the ratio of two integers. We’ve already seen that integers are rational numbers. The integer [latex]-8[/latex] could be written as the decimal [latex]-8.0[/latex]. So, clearly, some decimals are rational.

Think about the decimal [latex]7.3[/latex]. Can we write it as a ratio of two integers? Because [latex]7.3[/latex] means [latex]7\Large\frac{3}{10}[/latex], we can write it as an improper fraction, [latex]\Large\frac{73}{10}[/latex]. So [latex]7.3[/latex] is the ratio of the integers [latex]73[/latex] and [latex]10[/latex]. It is a rational number. In general, any decimal that ends after a number of digits such as [latex]7.3[/latex] or [latex]-1.2684[/latex] is a rational number. We can use the place value of the last digit as the denominator when writing the decimal as a fraction.

Irrational Numbers

We defined rational numbers as numbers that could be expressed as a fraction of two integers. Irrational numbers are numbers that cannot be expressed as a fraction of two integers. So irrational numbers must be those whose decimal representations do not terminate or become a repeating pattern.

irrational number

An irrational number is a number that cannot be written as the ratio of two integers. Its decimal form does not stop and does not repeat.

Let’s summarize a method we can use to determine whether a number is rational or irrational. If the decimal form of a number,

  • stops or repeats, the number is rational.
  • does not stop and does not repeat, the number is irrational.
Identify each of the following as rational or irrational:

  1. [latex]0.58\overline{3}[/latex]
  2. [latex]0.475[/latex]
  3. [latex]3.605551275\dots[/latex]

Another collection of irrational numbers is based on the special number, pi, denoted by the Greek letter [latex]\pi[/latex], which is the ratio of the circumference of the diameter of the circle. Any multiple or power of [latex]\pi[/latex] is an irrational number.

Real Numbers

We have seen that all counting numbers are whole numbers, all whole numbers are integers, and all integers are rational numbers. Irrational numbers are a separate category of their own. When we put together the rational numbers and the irrational numbers, we get the set of real numbers.

real numbers

Real numbers are numbers that are either rational or irrational.

This diagram illustrates the relationships between the different types of real numbers.

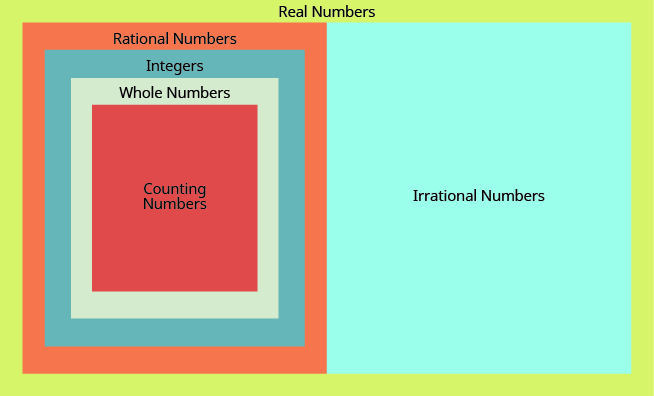
The image shows a large rectangle labeled real numbers. Inside this rectangle, there are two more rectangles labeled rational numbers and irrational numbers. Inside the rational numbers rectangle, there is a rectangle labeled integers. Inside of that rectangle, there is another rectangle labeled whole numbers. Inside of that rectangle is a square labeled counting numbers.

The real numbers can be visualized on a horizontal number line with an arbitrary point chosen as [latex]0[/latex], with negative numbers to the left of [latex]0[/latex] and positive numbers to the right of [latex]0[/latex]. A fixed unit distance is then used to mark off each integer (or other basic value) on either side of [latex]0[/latex]. Any real number corresponds to a unique position on the number line. The converse is also true: each location on the number line corresponds to exactly one real number. This is known as a one-to-one correspondence. We refer to this as the real number line.

A number line that is marked from negative five to five
The real number line
Does the term “real numbers” seem strange to you? Are there any numbers that are not “real”, and, if so, what could they be?For centuries, the only numbers people knew about were what we now call the real numbers. Then mathematicians discovered the set of imaginary numbers.An imaginary number is a number that, when squared, has a negative result, typically expressed as a real number multiplied by the imaginary unit [latex]i[/latex], where [latex]i^2=−1[/latex]. We won’t discuss imaginary numbers in this section, but you may encounter them in other places in this course.
Determine whether each of the numbers in the following list is a

  1. whole number
  2. integer
  3. rational number
  4. irrational number
  5. real number
[latex]-7[/latex], [latex]\frac{14}{5}[/latex], [latex]8[/latex], [latex]\sqrt{5}[/latex], [latex]5.9[/latex], [latex]-\sqrt{64}[/latex]

Sets of Numbers as Subsets

Beginning with the natural numbers, we have expanded each set to form a larger set, meaning that there is a subset relationship between the sets of numbers we have encountered so far. These relationships become more obvious when seen as a diagram.

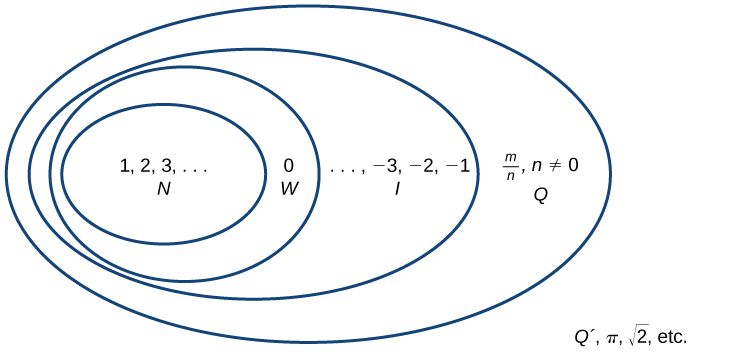
A large box labeled: Real Numbers encloses five circles. Four of these circles enclose each other and the other is separate from the rest. The innermost circle contains: 1, 2, 3… N. The circle enclosing that circle contains: 0 W. The circle enclosing that circle contains: …, -3, -2, -1 I. The outermost circle contains: m/n, n not equal to zero Q. The separate circle contains: pi, square root of two, etc Q´.
Sets of numbers.   N: the set of natural numbers   W: the set of whole numbers   I: the set of integers   Q: the set of rational numbers   Q´: the set of irrational numbers

sets of numbers

  • The set of natural numbers includes the numbers used for counting: [latex]\{1,2,3,\dots\}[/latex].
  • The set of whole numbers is the set of natural numbers plus zero: [latex]\{0,1,2,3,\dots\}[/latex].
  • The set of integers adds the negative natural numbers to the set of whole numbers: [latex]\{\dots,-3,-2,-1,0,1,2,3,\dots\}[/latex].
  • The set of rational numbers includes fractions written as [latex]\{\frac{m}{n}|m\text{ and }n\text{ are integers and }n\ne 0\}[/latex].
  • The set of irrational numbers is the set of numbers that are not rational, are nonrepeating, and are nonterminating: [latex]\{h|h\text{ is not a rational number}\}[/latex].