The concept of distance between two points in a Cartesian coordinate system is rooted in the Pythagorean Theorem, which is expressed as [latex]{a}^{2}+{b}^{2}={c}^{2}[/latex]. This based on a right triangle where [latex]a[/latex] and [latex]b[/latex] are the lengths of the legs adjacent to the right angle, and [latex]c[/latex] is the length of the hypotenuse.

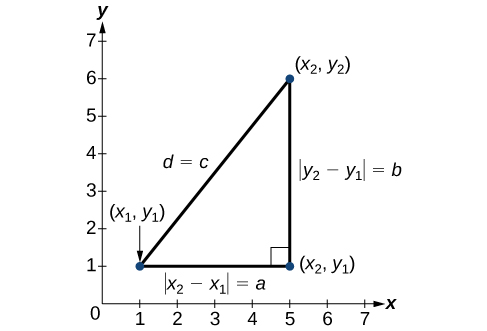
In the context of the coordinate plane, the lengths [latex]|{x}_{2}-{x}_{1}|[/latex] and [latex]|{y}_{2}-{y}_{1}|[/latex] correspond to [latex]a[/latex] and [latex]b[/latex], respectively. The distance [latex]d[/latex] between two points is analogous to [latex]c[/latex], the hypotenuse. The absolute value symbols ensure that these lengths are positive, as the absolute value of any number is positive.

To find [latex]c[/latex], or in our case [latex]d[/latex], the Pythagorean Theorem is rearranged as follows:

[latex]{c}^{2}={a}^{2}+{b}^{2}\rightarrow c=\sqrt{{a}^{2}+{b}^{2}}[/latex]

This leads us to the distance formula:

[latex]{d}^{2}={\left({x}_{2}-{x}_{1}\right)}^{2}+{\left({y}_{2}-{y}_{1}\right)}^{2}\to d=\sqrt{{\left({x}_{2}-{x}_{1}\right)}^{2}+{\left({y}_{2}-{y}_{1}\right)}^{2}}[/latex]

Note that the absolute value symbols are not necessary in this formula, as squaring any number results in a positive value.

Find the distance between the points [latex]\left(-3,-1\right)[/latex] and [latex]\left(2,3\right)[/latex].

Show Answer

Let us first look at the graph of the two points. Connect the points to form a right triangle.

 

Then, calculate the length of [latex]d[/latex] using the distance formula.

[latex]\begin{array}{l}d=\sqrt{{\left({x}_{2}-{x}_{1}\right)}^{2}+{\left({y}_{2}-{y}_{1}\right)}^{2}}\hfill \\ d=\sqrt{{\left(2-\left(-3\right)\right)}^{2}+{\left(3-\left(-1\right)\right)}^{2}}\hfill \\ =\sqrt{{\left(5\right)}^{2}+{\left(4\right)}^{2}}\hfill \\ =\sqrt{25+16}\hfill \\ =\sqrt{41}\hfill \end{array}[/latex]