Exponents and Scientific Notation: Learn It 1

  • Understand and use the rules for exponents
  • Change numbers between scientific notation and standard notation
  • Solve calculations using scientific notation

Exponential Notation

Exponential notation is a compact way to represent repeated multiplication of the same number. It’s a fundamental concept in mathematics that has significant implications across various disciplines, including science, finance, and technology.

In exponential notation, a number written with an exponent, like [latex]a^m[/latex], succinctly expresses that the base [latex]a[/latex] is multiplied by itself [latex]m[/latex] times. This notation is not only a shorthand for extensive multiplication but also a gateway to understanding more complex mathematical concepts like exponential functions and logarithms.

exponential notation

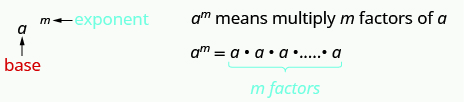
On the left side, a raised to the m is shown. The m is labeled in blue as an exponent. The a is labeled in red as the base. On the right, it says a to the m means multiply m factors of a. Below this, it says a to the m equals a times a times a times a, with m factors written below in blue.

 

This is read [latex]a[/latex] to the [latex]{m}^{\mathrm{th}}[/latex] power.

 

In the expression [latex]{a}^{m}[/latex], the exponent tells us how many times we use the base [latex]a[/latex] as a factor.

Negatives and exponents

Caution
Caution! Whether to include a negative sign as part of a base or not often leads to confusion. To clarify whether a negative sign is applied before or after the exponent, here is an example.

 

What is the difference in the way you would evaluate these two terms?

  1. [latex]-{3}^{2}[/latex]
  2. [latex]{\left(-3\right)}^{2}[/latex]

To evaluate 1), you would apply the exponent to the three first, then apply the negative sign last, like this:

 

[latex]\begin{array}{c}-\left({3}^{2}\right)\\=-\left(9\right) = -9\end{array}[/latex]

 

To evaluate 2), you would apply the exponent to the 3 and the negative sign:

 

[latex]\begin{array}{c}{\left(-3\right)}^{2}\\=\left(-3\right)\cdot\left(-3\right)\\={ 9}\end{array}[/latex]

 

The key to remembering this is to follow the order of operations. The first expression does not include parentheses so you would apply the exponent to the integer [latex]3[/latex] first, then apply the negative sign. The second expression includes parentheses, so hopefully you will remember that the negative sign also gets squared.

Evaluate Expressions With Exponents

Evaluating expressions containing exponents is the same as evaluating the linear expressions from earlier in the course. You substitute the value of the variable into the expression and simplify. So, when you evaluate the expression [latex]5x^{3}[/latex] if [latex]x=4[/latex], first substitute the value [latex]4[/latex] for the variable [latex]x[/latex]. Then evaluate, using order of operations.

Evaluate [latex]5x^{3}[/latex] if [latex]x=4[/latex].

In the example below, notice the how adding parentheses can change the outcome when you are simplifying terms with exponents.

Evaluate [latex]\left(5x\right)^{3}[/latex] if [latex]x=4[/latex].