Probability of Two Independent Events
Suppose we flipped a coin and rolled a die, and wanted to know the probability of getting a head on the coin and a [latex]6[/latex] on the die. Take a moment to think about how you could approach finding the probability. You could start by listing all the possible outcomes:
and determining the total number of outcomes. Notice, out of the twelve outcomes only one is the desired outcome, so the probability is [latex]\frac{1}{12}[/latex].
This example contains two independent events since getting a certain outcome from rolling a die had no influence on the outcome from flipping the coin. When two events are independent, the probability of both occurring is the product of the probabilities of the individual events.
independent events
Events [latex]A[/latex] and [latex]B[/latex] are independent events if the probability of event [latex]B[/latex] occurring is the same whether or not event [latex]A[/latex] occurs.
To multiply fractions, place the product of the numerators over the product of the denominators.
[latex]\dfrac{a}{b} \cdot \dfrac{c}{d} = \dfrac{ac}{bd}[/latex]
To write a fraction in reduced terms, first, take the prime factorization of the numerator and denominator, then cancel out factors that are common in the numerator and the denominator.
[latex]\dfrac{12}{18}=\dfrac{\cancel{2}\cdot 2\cdot \cancel{3}}{\cancel{2}\cdot 3\cdot \cancel{3}}=\dfrac{2}{3}[/latex]
In probability theory, just as we combine fractions through multiplication, we can combine the probabilities of independent events. For two independent events, [latex]A[/latex] and [latex]B[/latex], the probability of both occurring simultaneously is found by multiplying their individual probabilities. This principle is akin to multiplying fractions, where the product of the numerators over the product of the denominators gives the resulting fraction.
[latex]P(A \text{ and } B)[/latex] for independent events
If events [latex]A[/latex] and [latex]B[/latex] are independent, then the probability of both [latex]A[/latex] and [latex]B[/latex] occurring is
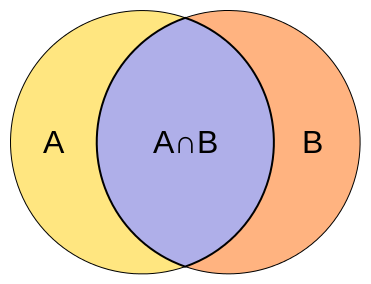
where [latex]P(A \text{ and } B)[/latex] is the probability of events [latex]A[/latex] and [latex]B[/latex] both occurring, [latex]P(A)[/latex] is the probability of event [latex]A[/latex] occurring, and [latex]P(B)[/latex] is the probability of event [latex]B[/latex] occurring
Notation: [latex]P\left(A\text{ and }B\right)[/latex] can also be notated as [latex]P(A \cap B)[/latex]
Moving from understanding individual event probabilities to exploring the likelihood of combined events, we encounter the concept of union in probability. If events [latex]A[/latex] and [latex]B[/latex] are independent, to determine the probability of either event occurring, we use the formula for the union of [latex]A[/latex] or [latex]B[/latex], which is [latex]P(A\text{ or }B)=P(A)+P(B)–P(A\text{ and }B)[/latex]. This formula accounts for the total probability of either event, minus the overlap where both events occur together, ensuring each possibility is counted only once.
[latex]P(A \text{ or } B)[/latex] for independent events
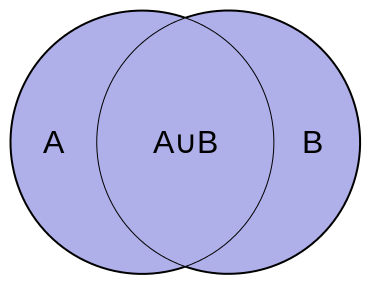
The probability of either [latex]A[/latex] or [latex]B[/latex] occurring (or both) is
[latex]P(A\text{ or }B)=P(A)+P(B)–P(A\text{ and }B)[/latex]
Notation: [latex]P\left(A\text{ or }B\right)[/latex] can also be notated as [latex]P(A \cup B)[/latex]