• Use prime factorization techniques to break down numbers into their prime factors.

What are Prime and Composite Numbers?

prime numbers

Prime Numbers are natural numbers greater than [latex]1[/latex] that have only two distinct positive divisors: [latex]1[/latex] and themselves.

This means they can only be divided evenly (without leaving a remainder) by 1 and the number itself. Prime numbers are the building blocks of all natural numbers because every number can be expressed as a product of primes.

Examples of Prime Numbers:[latex]2[/latex] (note: it is the only even prime number), [latex]3, 5, 7, 11, 29[/latex].

composite numbers

Composite Numbers are natural numbers that have more than two positive divisors.
a

In other words, aside from being divisible by [latex]1[/latex] and the number itself, composite numbers can be divided evenly by at least one other number.

Examples of Composite Numbers:[latex]4[/latex] (divisors: [latex]1, 2, 4[/latex]) and [latex]15[/latex] (divisors: [latex]1, 3, 5, 15[/latex])

The number [latex]1[/latex] is neither prime nor composite! It is unique in that it has only one positive divisor (itself).

Prime Factorization

The prime factorization of a number is the product of prime numbers that equals the number. You may want to refer to the following list of prime numbers less than [latex]50[/latex] as you work through this section.

[latex]2,3,5,7,11,13,17,19,23,29,31,37,41,43,47[/latex]

Memorizing the first five prime numbers —[latex]2, 3, 5, 7, 11[/latex]— will coming in handy when reducing fractions.

Prime Factorization Using the Factor Tree Method

One way to find the prime factorization of a number is to make a factor tree. We start by writing the number, and then writing it as the product of two factors. We write the factors below the number and connect them to the number with a small line segment—a “branch” of the factor tree. If a factor is prime, we circle it (like a bud on a tree), and do not factor that “branch” any further. If a factor is not prime, we repeat this process, writing it as the product of two factors and adding new branches to the tree. We continue until all the branches end with a prime. When the factor tree is complete, the circled primes give us the prime factorization. For example, let’s find the prime factorization of [latex]36[/latex]. We can start with any factor pair such as [latex]3[/latex] and [latex]12[/latex]. We write [latex]3[/latex] and [latex]12[/latex] below [latex]36[/latex] with branches connecting them.

 

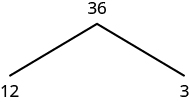
The factor [latex]3[/latex] is prime, so we circle it. The factor [latex]12[/latex] is composite, so we need to find its factors. Let’s use [latex]3[/latex] and [latex]4[/latex]. We write these factors on the tree under the [latex]12[/latex].

 

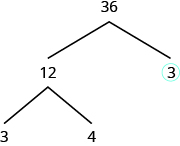
The factor [latex]3[/latex] is prime, so we circle it. The factor [latex]4[/latex] is composite, and it factors into [latex]2\cdot 2[/latex]. We write these factors under the [latex]4[/latex]. Since [latex]2[/latex] is prime, we circle both [latex]2\text{s}[/latex].

 

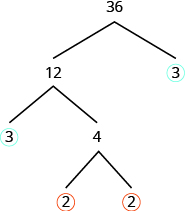
The prime factorization is the product of the circled primes. We generally write the prime factorization in order from least to greatest.

[latex]2\cdot 2\cdot 3\cdot 3[/latex]

In cases like this, where some of the prime factors are repeated, we can write prime factorization in exponential form.

[latex]\begin{array}{c}2\cdot 2\cdot 3\cdot 3\\ \\ {2}^{2}\cdot {3}^{2}\end{array}[/latex]

Note that we could have started our factor tree with any factor pair of [latex]36[/latex]. We chose [latex]12[/latex] and [latex]3[/latex], but the same result would have been the same if we had started with [latex]2[/latex] and [latex]18,4[/latex] and [latex]9[/latex], or [latex]6[/latex] and [latex]6[/latex].

How to: Find the prime factorization of a composite number using the tree method

1. Find any factor pair of the given number, and use these numbers to create two branches.
2. If a factor is prime, that branch is complete. Circle the prime.
3. If a factor is not prime, write it as the product of a factor pair and continue the process.
4. Write the composite number as the product of all the circled primes.

Let’s take a look at the number [latex]48[/latex].Note: We can also visualize the decomposition of a composite number into its prime components, much like creating a blueprint for a building but with numbers, using a factor tree. Each ‘branch’ of our factor tree represents a division by a prime factor.

Ask yourself, ‘What prime number is a factor of [latex]48[/latex]?’ Well, the smallest prime number is [latex]2[/latex]. Divide [latex]48[/latex] by [latex]2[/latex], giving you [latex]24[/latex].
Next, consider [latex]24[/latex]. It’s not a prime number, so what two numbers multiply to get[latex]24[/latex]? One option is [latex]4[/latex] and [latex]6[/latex].
Notice that [latex]4[/latex] is not a prime number, but can be broken down further into [latex]2[/latex] and [latex]2[/latex]. [latex]6[/latex] can also be decomposed. Break it down into [latex]2[/latex] and [latex]3[/latex], with 3 being a prime number.
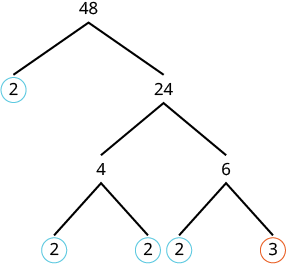We have fully factored down [latex]48[/latex] into its prime factors. Let’s write the product of all of the prime factors from least to greatest.	[latex]48 = 2\cdot 2\cdot 2\cdot 2\cdot 3[/latex] In exponential form: [latex]48 = 2^4 \cdot 3[/latex]