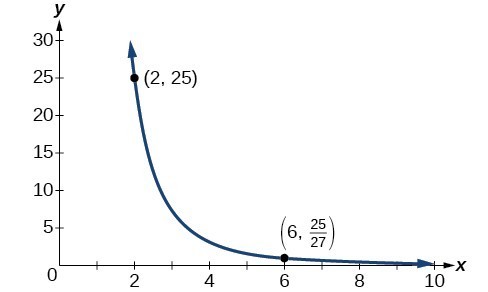
Inverse Variation
Inverse variation describes a relationship where one variable increases as the other decreases. This concept is crucial in understanding how different quantities affect each other inversely.
inverse variation
In an inverse variation, the relationship between two variables [latex]x[/latex] and [latex]y[/latex] can be expressed as:
[latex]y = \dfrac{k}{x^n}[/latex]
where [latex]k[/latex] is a nonzero constant, then we say that [latex]y[/latex] varies inversely with the power of [latex]x[/latex].
[latex]\\[/latex]
In inversely proportional relationships, or inverse variations, there is a constant multiple [latex]k = x^n \cdot y[/latex].
[latex]\\[/latex]
Consider the Atlantic Ocean, which covers [latex]22\%[/latex] of Earth’s surface. At a certain location, at the depth of [latex]500[/latex] feet, the temperature may be [latex]28^\circ\text{F}[/latex].If we create a table we observe that, as the depth increases, the water temperature decreases.
| [latex]d[/latex], depth | [latex]T=\frac{\text{14,000}}{d}[/latex] | Interpretation |
|---|---|---|
| [latex]500[/latex] ft | [latex]\frac{14,000}{500}=28[/latex] | At a depth of [latex]500[/latex] ft, the water temperature is [latex]28^\circ\text{F}[/latex]. |
| [latex]350[/latex] ft | [latex]\frac{14,000}{350}=40[/latex] | At a depth of [latex]350[/latex] ft, the water temperature is [latex]40^\circ\text{F}[/latex]. |
| [latex]250[/latex] ft | [latex]\frac{14,000}{250}=56[/latex] | At a depth of [latex]250[/latex] ft, the water temperature is [latex]56^\circ\text{F}[/latex]. |
We say the water temperature varies inversely with the depth of the water because, as the depth increases, the temperature decreases. The formula [latex]y=\dfrac{k}{x}[/latex] for inverse variation in this case uses [latex]k=14,000[/latex].
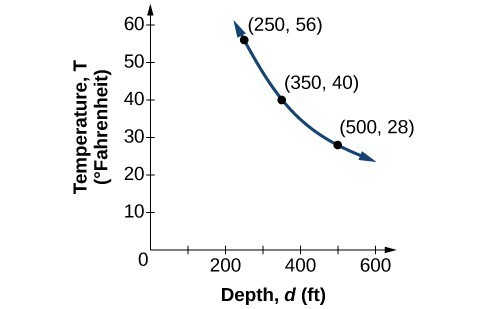
We notice in the relationship between these variables that, as one quantity increases, the other decreases. The two quantities are said to be inversely proportional and each term varies inversely with the other. Inversely proportional relationships are also called inverse variations.
- Identify the input, [latex]x[/latex], and the output, [latex]y[/latex].
- Determine the constant of variation. You may need to multiply [latex]y[/latex] by the specified power of [latex]x[/latex] to determine the constant of variation.
- Use the constant of variation to write an equation for the relationship.
- Substitute known values into the equation to find the unknown.