Transformations of Functions: Learn It 1

  • Shift graphs up, down, left, or right to understand how functions move on the coordinate plane
  • Flip graphs across the [latex]x[/latex]-axis or [latex]y[/latex]-axis to see how functions mirror themselves
  • Look at a graph to decide if a function is symmetrical around the [latex]y[/latex]-axis (even), the origin (odd), or not symmetrical at all
  • Apply compressions and stretches to function graphs
  • Use different moves and changes like shifting, flipping, squishing, and stretching on graphs

We all know that a flat mirror enables us to see an accurate image of ourselves and whatever is behind us. When we tilt the mirror, the images we see may shift horizontally or vertically. But what happens when we bend a flexible mirror? Like a carnival funhouse mirror, it presents us with a distorted image of ourselves, stretched or compressed horizontally or vertically. In a similar way, we can distort or transform mathematical functions to better adapt them to describing objects or processes in the real world.

Identifying Vertical Shifts

One simple kind of transformation involves shifting the entire graph of a function up and down, known as a vertical shift. 

vertical shift

A vertical shift occurs when you add or subtract a constant value to the function [latex]f(x)[/latex].

This shifts the graph of the function vertically without changing its shape.

  • Upward shift: If you add a constant [latex]c[/latex] to the function [latex]f(x)[/latex], the graph of the function shifts upward by [latex]c[/latex] units.

[latex]g(x) = f(x) +c[/latex]

  • Downward shift: If you subtract a constant [latex]c[/latex] to the function [latex]f(x)[/latex], the graph of the function shifts downward by [latex]c[/latex] units.

[latex]h(x) = f(x) -c[/latex]

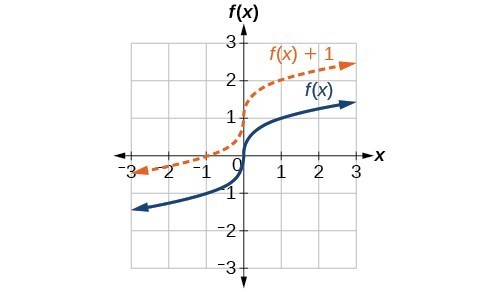
The image below shows the graph of a function [latex]f(x)[/latex] (solid blue line) and its vertically shifted version [latex]f(x) + 1[/latex] (dashed orange line).Graph of f of x equals the cubed root of x shifted upward one unit, the resulting graph passes through the point (0,1) instead of (0,0), (1, 2) instead of (1,1) and (-1, 0) instead of (-1, -1)Original Function [latex]f(x)[/latex]

  • The solid blue curve represents the original function [latex]\sqrt[3]{x}[/latex].
  • The function [latex]f(x)[/latex] passes through the origin [latex](0,0)[/latex] because [latex]\sqrt[3]{0} = 0[/latex].

Vertically Shifted Function [latex]f(x) + 1[/latex]

  • The dashed orange curve represents the function  [latex]f(x) + 1  = \sqrt[3]{x} + 1[/latex].
  • Each point on the graph of [latex]f(x) + 1[/latex] is exactly [latex]1[/latex] unit higher than the corresponding point on the graph of [latex]f(x)[/latex].
  • For example:
    • If [latex]x=0[/latex], then [latex]\sqrt[3]{0} +1 = 0 + 1  = 1[/latex].
    • If [latex]x=1[/latex], then [latex]\sqrt[3]{1} +1 = 1 + 1  = 2[/latex].

A vertical shift involves moving the graph of a function up or down without altering its shape. In this case, adding [latex]1[/latex] to the function [latex]f(x) = \sqrt[3]{x}[/latex] results in a vertical shift of the graph upward by [latex]1[/latex] unit.

A function [latex]f(x)[/latex] is given below. Create a table for the function [latex]g(x) = f(x)-3[/latex].

[latex]x[/latex] [latex]2[/latex] [latex]4[/latex] [latex]6[/latex] [latex]8[/latex]
[latex]f(x)[/latex] [latex]1[/latex] [latex]3[/latex] [latex]7[/latex] [latex]11[/latex]