Systems of Linear Equations: Three Variables: Learn It 1

  • Solve three equations with three different variables
  • Figure out when a set of three equations has no solution
  • Find and explain when a set of three equations has infinitely many solutions

Systems of Three Equations in Three Variables

A system of three equations in three variables helps us solve problems that involve three unknown quantities. Each equation in the system takes the form [latex]ax + by + cz = d[/latex], where [latex]x[/latex], [latex]y[/latex], and [latex]z[/latex] are the variables we’re solving for, and [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] are numbers that can’t all be zero. When we graph any single equation from this system, it creates a plane in three-dimensional space.

systems of three equations in three variables

A system of linear equations with three variables is a set of linear equations with three variables.

In order to solve systems of equations in three variables, known as three-by-three systems, the primary tool we will be using is called Gaussian elimination, named after the prolific German mathematician Karl Friedrich Gauss.

While there is no definitive order in which operations are to be performed, there are specific guidelines as to what type of moves can be made. We may number the equations to keep track of the steps we apply.

The goal is to eliminate one variable at a time to achieve upper triangular form, the ideal form for a three-by-three system because it allows for straightforward back-substitution to find a solution [latex](x,y,z)[/latex], which we call an ordered triple. A system in upper triangular form looks like the following:

[latex]\begin{align}Ax+By+Cz &=D \\ Ey+Fz &=G \\ Hz&=K\end{align}[/latex]

The third equation can be solved for [latex]z[/latex], and then we back-substitute to find [latex]y[/latex] and [latex]x[/latex].

To write the system in upper triangular form, we can perform the following operations:

  1. Interchange the order of any two equations.
  2. Multiply both sides of an equation by a nonzero constant.
  3. Add a nonzero multiple of one equation to another equation.

The solution set to a three-by-three system is an ordered triple [latex]{(x,y,z)}[/latex].

Number of Solutions

When we solve a system of linear equations with three variables, we have many possible solutions.

Graphically, if there is one solution, the ordered triple defines the point that is the intersection of three planes in space. You can visualize such an intersection by imagining any corner in a rectangular room. A corner is defined by three planes: two adjoining walls and the floor (or ceiling). Any point where two walls and the floor meet represents the intersection of three planes.

  • Systems that have a single solution is written as an ordered triple [latex]\left\{\left(x,y,z\right)\right\}[/latex].
  • Systems that have an infinite number of solutions are those which, after elimination, result in an identity expression that is always true, such as [latex]0=0[/latex].
  • Systems that have no solution are those that, after elimination, result in a statement that is a contradiction, such as [latex]3=0[/latex].

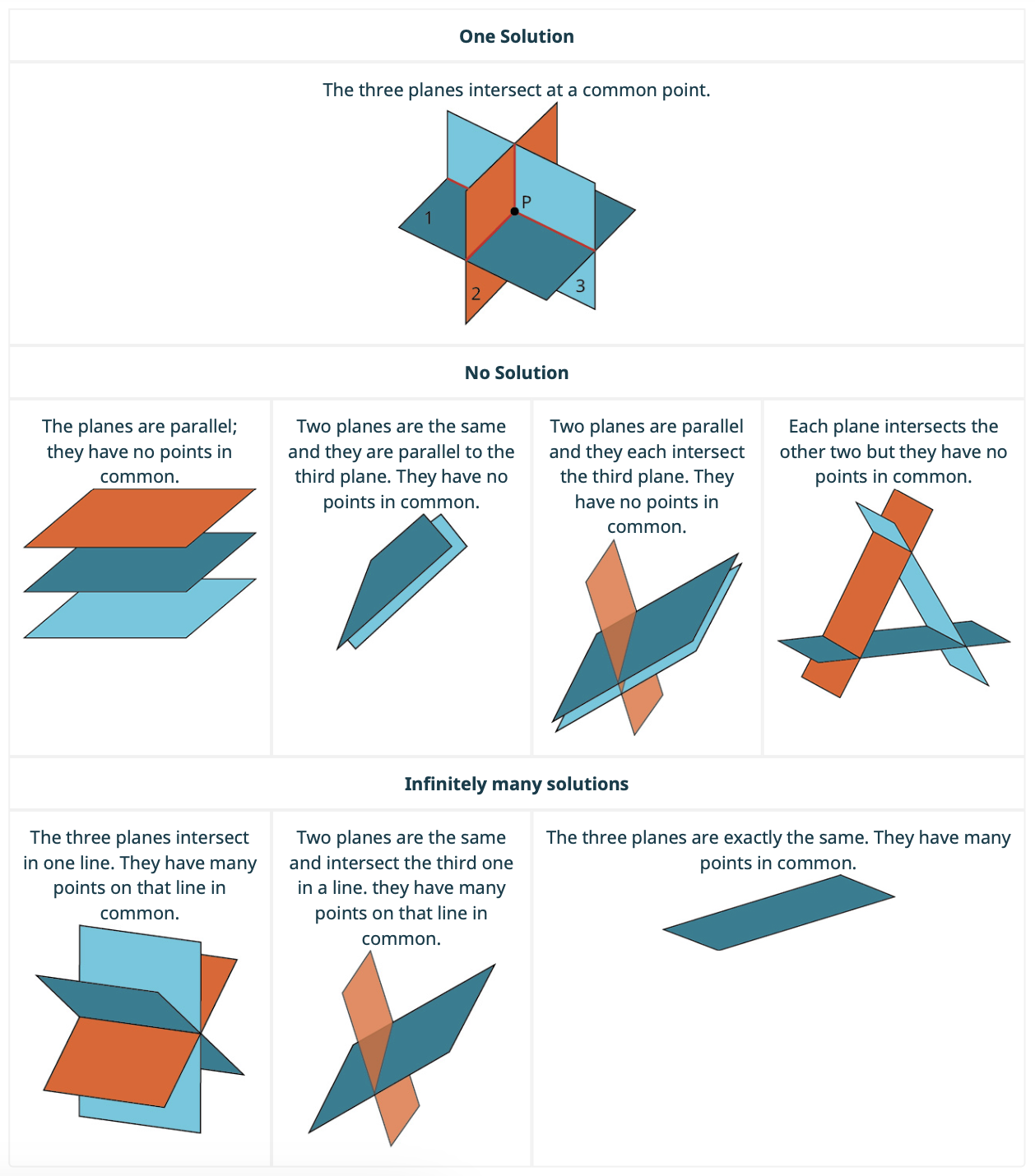
The solutions are summarized in the table below.

In the context of systems of equations, the terms “consistent,” “inconsistent,” and “dependent” are used to describe the nature of the solutions:

  1. Consistent System: A system of equations is consistent if it has at least one solution. This can be either a single unique solution or infinitely many solutions.
  2. Inconsistent System: A system of equations is inconsistent if it has no solutions. This occurs when the equations represent parallel lines that never intersect.
  3. Dependent System: A system of equations is dependent if it has infinitely many solutions. This occurs when the equations represent the same line (they are essentially the same equation written in different forms).