- Use summation notation to write a sum for a series
- Use the formula for the sum of the first [latex]n[/latex] terms of an arithmetic series
- Use the formula for the sum of the first [latex]n[/latex] terms of a geometric series
- Use the formula to accurately find the sum of an infinite geometric series
- Solve annuity problems by applying concepts of regular series additions
Series and Summation Notation
Now that we’ve explored sequences, let’s take it a step further and talk about series. While a sequence lists numbers in a specific order, a series is what you get when you add those numbers together. In other words, a series is the sum of the terms in a sequence. Understanding how to work with series is important because it allows us to find the total of a sequence of numbers, which has many practical applications in mathematics and beyond.
Summation notation is used to represent series. Summation notation is often known as sigma notation because it uses the Greek capital letter sigma, [latex]\Sigma[/latex], to represent the sum. Summation notation includes an explicit formula and specifies the first and last terms in the series. An explicit formula for each term of the series is given to the right of the sigma. A variable called the index of summation is written below the sigma. The index of summation is set equal to the lower limit of summation, which is the number used to generate the first term in the series. The number above the sigma, called the upper limit of summation, is the number used to generate the last term in a series.
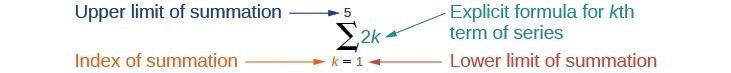
If we interpret the given notation, we see that it asks us to find the sum of the terms in the series [latex]{a}_{k}=2k[/latex] for [latex]k=1[/latex] through [latex]k=5[/latex]. We can begin by substituting the terms for [latex]k[/latex] and listing out the terms of this series.
[latex]\begin{align} &{a}_{1}=2\left(1\right)=2 \\ &{a}_{2}=2\left(2\right)=4 \\ &{a}_{3}=2\left(3\right)=6 \\ &{a}_{4}=2\left(4\right)=8 \\ &{a}_{5}=2\left(5\right)=10 \end{align}[/latex]
We can find the sum of the series by adding the terms:
[latex]\sum\limits _{k=1}^{5}2k=2+4+6+8+10=30[/latex]
summation notation
The sum of the first [latex]n[/latex] terms of a series can be expressed in summation notation as follows:
[latex]\sum\limits _{k=1}^{n}{a}_{k}[/latex]
This notation tells us to find the sum of [latex]{a}_{k}[/latex] from
[latex]k=1[/latex] to [latex]k=n[/latex].
[latex]k[/latex] is called the index of summation, 1 is the lower limit of summation, and [latex]n[/latex] is the upper limit of summation.
- Identify the lower limit of summation.
- Identify the upper limit of summation.
- Substitute each value of [latex]k[/latex] from the lower limit to the upper limit into the formula.
- Add to find the sum.