Recursive Formula

Now that we’ve covered explicit formulas, let’s talk about another way to define sequences: the recursive formula. Unlike the explicit formula, which gives you a direct way to find any term in the sequence, a recursive formula builds each term based on the one before it. In other words, you need to know the previous term(s) to find the next one.

Recursive formulas are especially useful when the sequence is defined by a step-by-step process or when each term depends on its predecessor. While it might seem a bit more complex, recursive formulas can be powerful tools for understanding and working with sequences.

Do you notice how the sequence seems to mirror patterns found in nature?
[latex]\\[/latex]
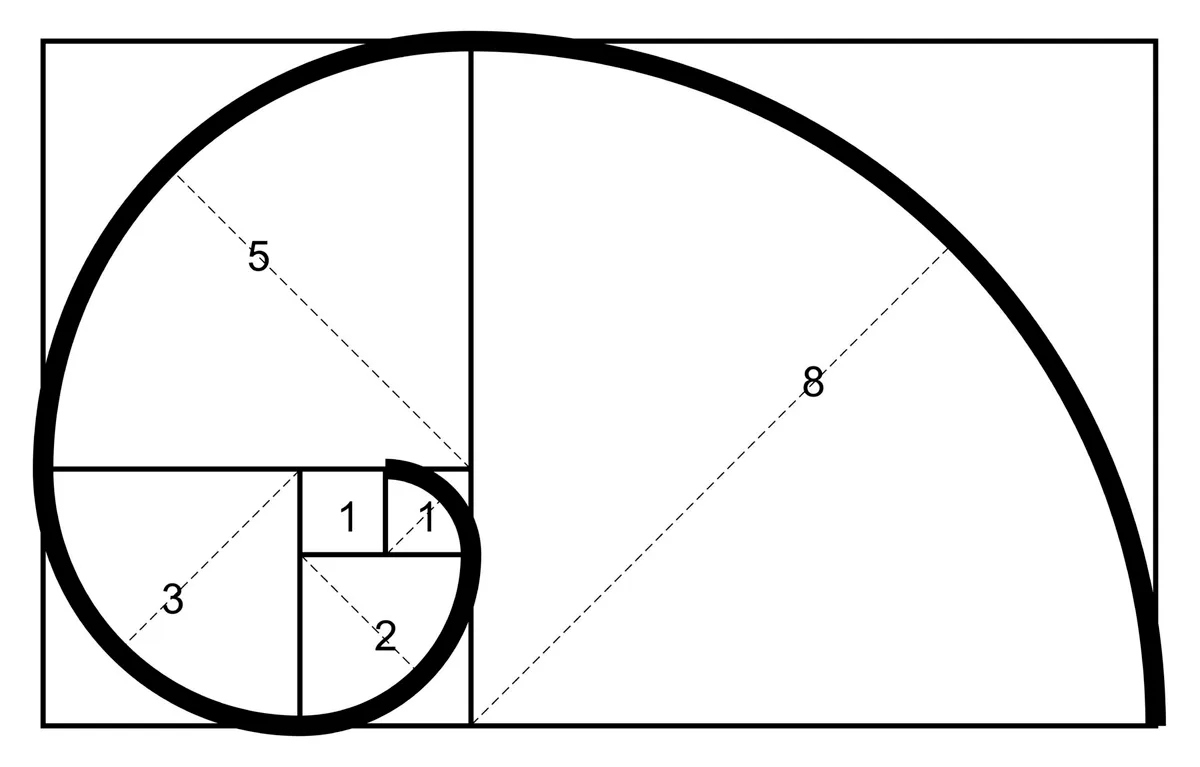
The Fibonacci sequence isn’t just a mathematical curiosity—it’s a fundamental part of the world around us. From the spirals of shells to the branching of trees, this sequence helps explain the structure and growth patterns of various natural forms. What’s fascinating is that each term relies on the ones before it, creating a beautiful and interconnected pattern that we can observe in so many living things. This dependency makes the Fibonacci sequence unique, as it’s best described by a recursive formula rather than an explicit one.
[latex]\\[/latex]
Fibonacci sequence is [latex]1, 1, 2, 3, 5, 8, 13, 21, 34,….[/latex].
[latex]\\[/latex]
Each number in the sequence is the sum of the two preceding ones, starting from [latex]1[/latex] and [latex]1[/latex]. This sequence is unique because of its recursive nature, meaning each term is defined by the terms that came before it.The formula for the Fibonacci sequence is:

• [latex]F_1 = 1[/latex]
• [latex]F_2 = 1[/latex]
• [latex]F_n = F_{n-1}+F_{n-2}[/latex], for [latex]n \ge 3[/latex]