- Use arrow notation to describe how rational functions behave at different points
- Apply rational functions to solve real-world problems
- Find out which values are allowed for rational functions and understand what limits these values set
- Spot where rational functions shoot up to infinity (vertical asymptotes) and explore why these points are important
- Find where rational functions level off at infinity (horizontal asymptotes) and see how these affect the graph
- Draw graphs of rational functions carefully, including places where the graph breaks or levels out, and where it’s not defined
Rational Functions
The Main Idea
- Definition:
- A rational function is a quotient of two polynomial functions: [latex]f(x) = \frac{P(x)}{Q(x)}[/latex], where [latex]Q(x) \neq 0[/latex]
- Domain:
- Includes all real numbers except where [latex]Q(x) = 0[/latex]
- Zero in the denominator makes the function undefined
- Behavior near vertical asymptotes:
- Function values approach infinity or negative infinity as [latex]x[/latex] approaches points where [latex]Q(x) = 0[/latex]
- End behavior:
- Determined by the degrees of [latex]P(x)[/latex] and [latex]Q(x)[/latex]
- May approach a horizontal asymptote as [latex]x[/latex] approaches infinity
- Arrow notation:
- Used to describe function behavior as [latex]x[/latex] approaches specific values or infinity
- Arrow notation shortcuts:
- [latex]x \to a^-[/latex]: x approaches a from the left
- [latex]x \to a^+[/latex]: x approaches a from the right
- [latex]x \to \pm\infty[/latex]: x approaches positive/negative infinity
- [latex]f(x) \to \pm\infty[/latex]: function values increase/decrease without bound
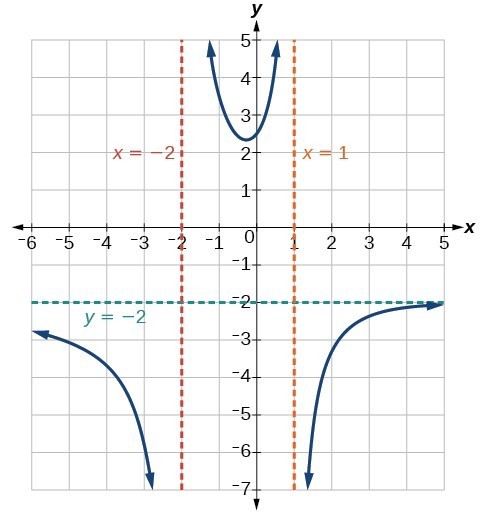
Local and End Behavior of [latex]f\left(x\right)=\frac{1}{x}[/latex]
- Vertical Asymptotes:
- Occur when the denominator equals zero
- Represent local behavior near undefined points
- Horizontal Asymptotes:
- Represent end behavior as [latex]x[/latex] approaches infinity or negative infinity
- Determined by comparing degrees of numerator and denominator
- End Behavior:
- Describes function behavior for very large positive or negative [latex]x[/latex] values
- Arrow Notation:
- Used to concisely describe limits and asymptotic behavior
You can view the transcript for “Arrow Notation” here (opens in new window).
Domain and Its Effect on Vertical Asymptotes
The Main Idea
- Domain of Rational Functions:
- Includes all real numbers except those that make the denominator zero
- Vertical Asymptotes:
- Occur when the denominator equals zero
- Represent values where the function is undefined
- Removable Discontinuities:
- Occur when a factor cancels out between numerator and denominator
- Create “holes” in the graph
- Factoring:
- Essential for identifying both vertical asymptotes and removable discontinuities
- Graphical Representation:
- Vertical asymptotes: function approaches infinity
- Removable discontinuities: open circles on the graph
Watch the following video to see more examples of finding the domain of a rational function.
You can view the transcript for “Ex: The Domain of Rational Functions” here (opens in new window).
Horizontal Asymptotes and Intercepts
The Main Idea
- End Behavior:
- Describes how a function behaves as [latex]x[/latex] approaches positive or negative infinity
- For rational functions, determined by the ratio of leading terms in numerator and denominator
- Horizontal Asymptotes:
- Represent the [latex]y[/latex]-value the function approaches as [latex]x[/latex] approaches infinity
- Determined by comparing degrees of numerator and denominator
- Three Cases for Horizontal Asymptotes:
- Case [latex]1[/latex]: Degree(numerator) [latex]<[/latex] Degree(denominator)
- Case [latex]2[/latex]: Degree(numerator) [latex]>[/latex] Degree(denominator)
- Case [latex]3[/latex]: Degree(numerator) [latex]=[/latex] Degree(denominator)
- Slant Asymptotes:
- Occur when degree of numerator is exactly one more than degree of denominator
- Crossing Asymptotes:
- Rational functions can cross horizontal asymptotes, unlike vertical asymptotes
- Vertical Intercept ([latex]y[/latex]-intercept):
- Found by evaluating the function at [latex]x = 0[/latex]
- May not exist if the function is undefined at [latex]x = 0[/latex]
- Horizontal Intercepts ([latex]x[/latex]-intercepts):
- Found by solving [latex]r(x) = 0[/latex]
- Occur when the numerator equals zero (if the denominator is not also zero)
- Existence of Intercepts:
- A rational function may not have vertical or horizontal intercepts
How to Find Intercepts
- [latex]y[/latex]-intercept:
- Evaluate [latex]r(0)[/latex] by substituting [latex]0[/latex] for all [latex]x[/latex] in the function
- If defined, the y-intercept is [latex](0, r(0))[/latex]
- x-intercepts:
- Set the numerator equal to zero and solve for [latex]x[/latex]
- Check that these [latex]x[/latex]-values don’t make the denominator zero
- The [latex]x[/latex]-intercepts are [latex](x, 0)[/latex] for each valid solution
[latex]f\left(x\right)=\dfrac{\left(2x - 1\right)\left(2x+1\right)}{\left(x - 2\right)\left(x+3\right)}[/latex]
Watch this video to see more worked examples of determining which kind of horizontal asymptote a rational function will have.
You can view the transcript for “Ex: Determine Horizontal Asymptotes of Rational Functions” here (opens in new window).
Watch the following video to see more worked examples of finding asymptotes, intercepts and holes of rational functions.
You can view the transcript for “Ex: Find the Intercepts, Asymptotes, and Hole of a Rational Function” here (opens in new window).
Graphing Rational Functions
The Main Idea
- Numerator and Denominator Roles:
- Numerator reveals [latex]x[/latex]-intercepts
- Denominator reveals vertical asymptotes
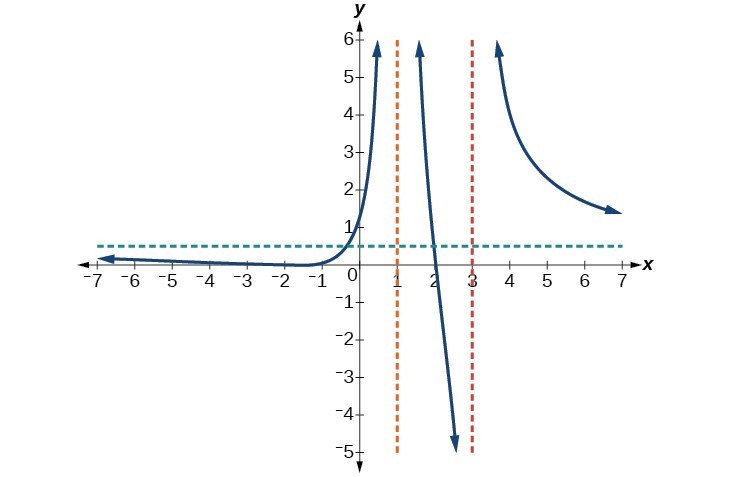
- Effect of Factor Powers:
- Factors with powers [latex]> 1[/latex] affect graph shape at intercepts
- Odd-degree factors in denominator: opposite behavior on either side of asymptote
- Even-degree factors in denominator: same behavior on both sides of asymptote
- Vertical Asymptote Behavior:
- Odd-degree factor: graph approaches positive infinity on one side, negative infinity on the other
- Even-degree factor: graph approaches either positive or negative infinity on both sides
Step-by-Step Graphing Process
- Simplify the Function:
- Factor and reduce common terms in numerator and denominator
- Find the Domain:
- Identify [latex]x[/latex]-values where denominator equals zero
- Identify Vertical Asymptotes and Holes:
- Set denominator to zero and solve for [latex]x[/latex]
- Check if numerator is also zero at these [latex]x[/latex]-values (indicates holes, not asymptotes)
- Find Horizontal or Slant Asymptote:
- Compare degrees of numerator ([latex]n[/latex]) and denominator ([latex]d[/latex]):
- If [latex]n < d[/latex]: Horizontal asymptote at [latex]y = 0[/latex]
- If [latex]n = d[/latex]: Horizontal asymptote at [latex]y[/latex] = ratio of leading coefficients
- If [latex]n = d + 1[/latex]: Slant asymptote (find using polynomial long division)
- Compare degrees of numerator ([latex]n[/latex]) and denominator ([latex]d[/latex]):
- Find Intercepts:
- [latex]x[/latex]-intercepts: Set numerator to zero, solve for [latex]x[/latex]
- [latex]y[/latex]-intercept: Evaluate function at [latex]x = 0[/latex]
- Plot Key Points:
- Calculate points on both sides of vertical asymptotes
- Sketch the Graph:
- Draw asymptotes (dashed lines)
- Plot intercepts and key points
- Draw curve, ensuring proper asymptote behavior
Watch the following video to see another worked example of how to match different kinds of rational functions with their graphs.
You can view the transcript for “Ex: Match Equations of Rational Functions to Graphs” here (opens in new window).
Writing Rational Functions
The Main Idea
- Relationship between graph features and function components:
- [latex]x[/latex]-intercepts correspond to factors in the numerator
- Vertical asymptotes correspond to factors in the denominator
- General form of a rational function: [latex]f(x) = a\frac{(x-x_1)^{p_1}(x-x_2)^{p_2}\cdots(x-x_n)^{p_n}}{(x-v_1)^{q_1}(x-v_2)^{q_2}\cdots(x-v_m)^{q_m}}[/latex] Where:
- [latex]x_i[/latex] are [latex]x[/latex]-intercepts
- [latex]v_j[/latex] are vertical asymptotes
- [latex]p_i[/latex] and [latex]q_j[/latex] are multiplicities
- [latex]a[/latex] is the stretch factor
- Behavior at intercepts and asymptotes determines multiplicities
- Any point on the graph satisfies the function equation
Step-by-Step Process
- Identify [latex]x[/latex]-intercepts:
- Locate where graph crosses [latex]x[/latex]-axis
- Determine multiplicity based on behavior (passing through or bouncing)
- Identify vertical asymptotes:
- Locate where graph approaches infinity
- Determine multiplicity based on behavior on each side
- Write the general form:
- Use [latex]x[/latex]-intercepts for numerator factors
- Use vertical asymptotes for denominator factors
- Determine stretch factor [latex]a[/latex]:
- Use a clear point on the graph, often the [latex]y[/latex]-intercept
- Substitute point into the function and solve for [latex]a[/latex]
You can view the transcript for “Ex 1: Find the Equation of Rational Function From a Graph” here (opens in new window).