Rational Functions

For the following exercises, find the domain of the rational functions.

1. [latex]f(x)=\dfrac{x+1}{x^2-1}[/latex]
2. [latex]f(x)=\dfrac{x^2+4x-3}{x^4-5x^2+4}[/latex]

For the following exercises, find the domain, vertical asymptotes, and horizontal asymptotes of the functions.

3. [latex]f(x)=\dfrac{2}{5x+2}[/latex]
4. [latex]f(x)=\dfrac{x}{x^2+5x-36}[/latex]
5. [latex]f(x)=\dfrac{3x-4}{x^3-16x}[/latex]
6. [latex]f(x)=\dfrac{x+5}{x^2-25}[/latex]
7. [latex]f(x)=\dfrac{4-2x}{3x-1}[/latex]

For the following exercises, find the x- and y-intercepts for the functions.

8. [latex]f(x)=\dfrac{x}{x^2-x}[/latex]
9. [latex]f(x)=\dfrac{x^2+x+6}{x^2-10x+24}[/latex]

For the following exercises, describe the local and end behavior of the functions.

10. [latex]f(x)=\dfrac{x}{2x+1}[/latex]
11. [latex]f(x)=\dfrac{-2x}{x-6}[/latex]
12. [latex]f(x)=\dfrac{2x^2-32}{6x^2+13x-5}[/latex]

For the following exercises, find the slant asymptote of the functions.

13. [latex]f(x)=\dfrac{4x^2-10}{2x-4}[/latex]
14. [latex]f(x)=\dfrac{6x^3-5x}{3x^2+4}[/latex]

For the following exercises, find the horizontal intercepts, the vertical intercept, the vertical asymptotes, and the horizontal or slant asymptote of the functions. Use that information to sketch a graph.

15. [latex]p(x)=\dfrac{2x-3}{x+4}[/latex]
16. [latex]s(x)=\dfrac{4}{(x-2)^2}[/latex]
17. [latex]f(x)=\dfrac{3x^2-14x-5}{3x^2+8x-16}[/latex]
18. [latex]a(x)=\dfrac{x^2+2x-3}{x^2-1}[/latex]

For the following exercises, write an equation for a rational function with the given characteristics.

19. Vertical asymptotes at [latex]x=5[/latex] and [latex]x=-5[/latex], [latex]x[/latex]-intercepts at [latex](2,0)[/latex] and [latex](-1,0)[/latex], [latex]y[/latex]-intercept at [latex](0,4)[/latex]
20. Vertical asymptotes at [latex]x=-4[/latex] and [latex]x=-5[/latex], [latex]x[/latex]-intercepts at [latex](4,0)[/latex] and [latex](-6,0)[/latex], Horizontal asymptote at [latex]y=7[/latex]
21. Vertical asymptote at [latex]x=-1[/latex], Double zero at [latex]x=2[/latex], [latex]y[/latex]-intercept at [latex](0,2)[/latex]

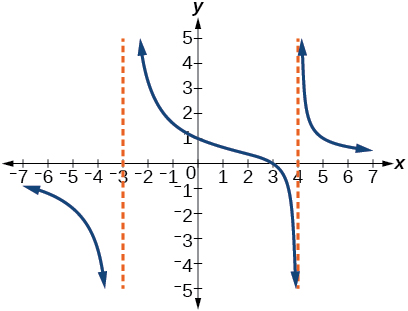
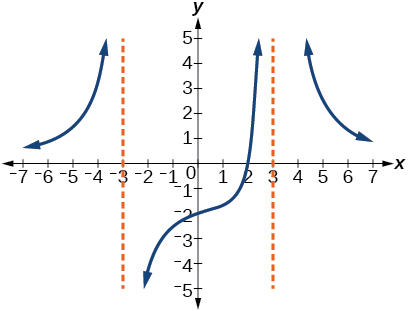
For the following exercises, use the graphs to write an equation for the function.

22. 
23. 

For the following exercise, express a rational function that describes the situation.

24. In the refugee camp hospital, a large mixing tank currently contains [latex]300[/latex] gallons of water, into which [latex]8[/latex] pounds of sugar have been mixed. A tap will open, pouring [latex]20[/latex] gallons of water per minute into the tank at the same time sugar is poured into the tank at a rate of [latex]2[/latex] pounds per minute. Find the concentration (pounds per gallon) of sugar in the tank after [latex]t[/latex] minutes.

For the following exercise, use the given rational function to answer the question.

25. The concentration [latex]C[/latex] of a drug in a patient’s bloodstream [latex]t[/latex] hours after injection is given by [latex]C(t)=\dfrac{100t}{2t^2+75}[/latex]. Use a calculator to approximate the time when the concentration is highest.

For the following exercises, construct a rational function that will help solve the problem. Then, use a calculator to answer the question.

26. A rectangular box with a square base is to have a volume of [latex]20[/latex] cubic feet. The material for the base costs [latex]30[/latex] cents/square foot. The material for the sides costs [latex]10[/latex] cents/square foot. The material for the top costs [latex]20[/latex] cents/square foot. Determine the dimensions that will yield minimum cost. Let [latex]x[/latex] = length of the side of the base.
27. A right circular cylinder with no top has a volume of [latex]50[/latex] cubic meters. Find the radius that will yield minimum surface area. Let [latex]x[/latex] = radius.

Inverses and Radical Functions

For the following exercises, find the inverse of the function on the given domain.

1. [latex]f(x)=(x-4)^2, [4,\infty)[/latex]
2. [latex]f(x)=(x+1)^2-3, [-1,\infty)[/latex]
3. [latex]f(x)=12-x^2, [0,\infty)[/latex]
4. [latex]f(x)=2x^2+4, [0,\infty)[/latex]

For the following exercises, find the inverse of the functions.

5. [latex]f(x)=3x^3+1[/latex]
6. [latex]f(x)=4-2x^3[/latex]

For the following exercises, find the inverse of the functions.

7. [latex]f(x)=\sqrt{3-4x}[/latex]
8. [latex]f(x)=\sqrt{6x-8}+5[/latex]
9. [latex]f(x)=3-\sqrt[3]{x}[/latex]
10. [latex]f(x)=\dfrac{3}{x-4}[/latex]
11. [latex]f(x)=\dfrac{x-2}{x+7}[/latex]
12. [latex]f(x)=\dfrac{5x+1}{2-5x}[/latex]
13. [latex]f(x)=x^2+4x+1, [-2,\infty)[/latex]

For the following exercises, find the inverse of the function and graph both the function and its inverse.

14. [latex]f(x)=x^2+2, x \geq 0[/latex]
15. [latex]f(x)=(x+3)^2, x \geq -3[/latex]
16. [latex]f(x)=x^3+3[/latex]

For the following exercises, use a graph to help determine the domain of the functions.

17. [latex]f(x)=\sqrt{\dfrac{(x+1)(x-1)}{x}}[/latex]
18. [latex]f(x)=\sqrt{\dfrac{x(x+3)}{x-4}}[/latex]
19. [latex]f(x)=\sqrt{\dfrac{9-x^2}{x+4}}[/latex]

For the following exercises, determine the function described and then use it to answer the question.

20. An object dropped from a height of [latex]600[/latex] feet has a height, [latex]h(t)[/latex], in feet after [latex]t[/latex] seconds have elapsed, such that [latex]h(t)=600-16t^2[/latex]. Express [latex]t[/latex] as a function of height [latex]h[/latex], and find the time to reach a height of [latex]400[/latex] feet.
21. The surface area, [latex]A[/latex], of a sphere in terms of its radius, [latex]r[/latex], is given by [latex]A(r)=4\pi r^2[/latex]. Express [latex]r[/latex] as a function of [latex]A[/latex], and find the radius of a sphere with a surface area of [latex]1000[/latex] square inches.
22. The period [latex]T[/latex], in seconds, of a simple pendulum as a function of its length [latex]l[/latex], in feet, is given by [latex]T(l)=2\pi\sqrt{\dfrac{l}{32.2}}[/latex]. Express [latex]l[/latex] as a function of [latex]T[/latex] and determine the length of a pendulum with period of [latex]2[/latex] seconds.
23. The surface area, [latex]A[/latex], of a cylinder in terms of its radius, [latex]r[/latex], and height, [latex]h[/latex], is given by [latex]A=2\pi r^2+2\pi rh[/latex]. If the height of the cylinder is [latex]4[/latex] feet, express the radius as a function of [latex]A[/latex] and find the radius if the surface area is [latex]200[/latex] square feet.
24. Consider a cone with height of [latex]30[/latex] feet. Express the radius, [latex]r[/latex], in terms of the volume, [latex]V[/latex], and find the radius of a cone with volume of [latex]1000[/latex] cubic feet.

Variations

For the following exercises, write an equation describing the relationship of the given variables.

1. [latex]y[/latex] varies directly as the square of [latex]x[/latex] and when [latex]x=4[/latex], [latex]y=80[/latex].
2. [latex]y[/latex] varies directly as the cube of [latex]x[/latex] and when [latex]x=36[/latex], [latex]y=24[/latex].
3. [latex]y[/latex] varies directly as the fourth power of [latex]x[/latex] and when [latex]x=1[/latex], [latex]y=6[/latex].
4. [latex]y[/latex] varies inversely as the square of [latex]x[/latex] and when [latex]x=3[/latex], [latex]y=2[/latex].
5. [latex]y[/latex] varies inversely as the fourth power of [latex]x[/latex] and when [latex]x=3[/latex], [latex]y=1[/latex].
6. [latex]y[/latex] varies inversely as the cube root of [latex]x[/latex] and when [latex]x=64[/latex], [latex]y=5[/latex].
7. [latex]y[/latex] varies jointly as [latex]x[/latex], [latex]z[/latex], and [latex]w[/latex] and when [latex]x=1[/latex], [latex]z=2[/latex], [latex]w=5[/latex], then [latex]y=100[/latex].
8. [latex]y[/latex] varies jointly as [latex]x[/latex] and the square root of [latex]z[/latex] and when [latex]x=2[/latex] and [latex]z=25[/latex], then [latex]y=100[/latex].
9. [latex]y[/latex] varies jointly as [latex]x[/latex] and [latex]z[/latex] and inversely as [latex]w[/latex]. When [latex]x=3[/latex], [latex]z=5[/latex], and [latex]w=6[/latex], then [latex]y=10[/latex].
10. [latex]y[/latex] varies jointly as [latex]x[/latex] and [latex]z[/latex] and inversely as the square root of [latex]w[/latex] and the square of [latex]t[/latex]. When [latex]x=3[/latex], [latex]z=1[/latex], [latex]w=25[/latex], and [latex]t=2[/latex], then [latex]y=6[/latex].

For the following exercises, use the given information to find the unknown value.

11. [latex]y[/latex] varies directly as the square of [latex]x[/latex]. When [latex]x=2[/latex], then [latex]y=16[/latex]. Find [latex]y[/latex] when [latex]x=8[/latex].
12. [latex]y[/latex] varies directly as the square root of [latex]x[/latex]. When [latex]x=16[/latex], then [latex]y=4[/latex]. Find [latex]y[/latex] when [latex]x=36[/latex].
13. [latex]y[/latex] varies inversely with [latex]x[/latex]. When [latex]x=3[/latex], then [latex]y=2[/latex]. Find [latex]y[/latex] when [latex]x=1[/latex].
14. [latex]y[/latex] varies inversely with the cube of [latex]x[/latex]. When [latex]x=3[/latex], then [latex]y=1[/latex]. Find [latex]y[/latex] when [latex]x=1[/latex].
15. [latex]y[/latex] varies inversely with the cube root of [latex]x[/latex]. When [latex]x=27[/latex], then [latex]y=5[/latex]. Find [latex]y[/latex] when [latex]x=125[/latex].
16. [latex]y[/latex] varies jointly as [latex]x[/latex], [latex]z[/latex], and [latex]w[/latex]. When [latex]x=2[/latex], [latex]z=1[/latex], and [latex]w=12[/latex], then [latex]y=72[/latex]. Find [latex]y[/latex] when [latex]x=1[/latex], [latex]z=2[/latex], and [latex]w=3[/latex].
17. [latex]y[/latex] varies jointly as [latex]x[/latex] and [latex]z[/latex] and inversely as [latex]w[/latex]. When [latex]x=5[/latex], [latex]z=2[/latex], and [latex]w=20[/latex], then [latex]y=4[/latex]. Find [latex]y[/latex] when [latex]x=3[/latex] and [latex]z=8[/latex], and [latex]w=48[/latex].
18. [latex]y[/latex] varies jointly as the square of [latex]x[/latex] and the cube of [latex]z[/latex] and inversely as the square root of [latex]w[/latex]. When [latex]x=2[/latex], [latex]z=2[/latex], and [latex]w=64[/latex], then [latex]y=12[/latex]. Find [latex]y[/latex] when [latex]x=1[/latex], [latex]z=3[/latex], and [latex]w=4[/latex].

For the following exercises, use the given information to answer the questions.

19. The distance [latex]s[/latex] that an object falls varies directly with the square of the time, [latex]t[/latex], of the fall. If an object falls [latex]16[/latex] feet in [latex]1[/latex] second, how long for it to fall [latex]144[/latex] feet?
20. The rate of vibration of a string under constant tension varies inversely with the length of the string. If a string is [latex]24[/latex] inches long and vibrates [latex]128[/latex] times per second, what is the length of a string that vibrates [latex]64[/latex] times per second?
21. The weight of an object above the surface of Earth varies inversely with the square of the distance from the center of Earth. If a body weighs [latex]50[/latex] pounds when it is [latex]3960[/latex] miles from Earth’s center, what would it weigh if it were [latex]3970[/latex] miles from Earth’s center?
22. The current in a circuit varies inversely with its resistance measured in ohms. When the current in a circuit is [latex]40[/latex] amperes, the resistance is [latex]10[/latex] ohms. Find the current if the resistance is [latex]12[/latex] ohms.
23. The horsepower (hp) that a shaft can safely transmit varies jointly with its speed (in revolutions per minute (rpm) and the cube of the diameter. If the shaft of a certain material [latex]3[/latex] inches in diameter can transmit [latex]45[/latex] hp at [latex]100[/latex] rpm, what must the diameter be in order to transmit [latex]60[/latex] hp at [latex]150[/latex] rpm?