- Learn how to find the inverse (or “reverse”) of a polynomial function when it’s possible
- Figure out how to limit the domain of a polynomial function so you can find its inverse
- Use radical functions to solve real-world problems
Radical Functions
Imagine you’re designing a new smartphone app that adjusts screen brightness based on ambient light. You’ve found that the relationship between light intensity and ideal brightness follows a cubic function:
[latex]f(x) = 0.1x^3 + 1[/latex]
where [latex]x[/latex] is the light intensity and [latex]f(x)[/latex] is the ideal brightness setting.
But what if you want your app to do the reverse – determine the light intensity when given a brightness setting? This is where radical functions come into play.
Radical functions are like the “undo” button for certain polynomial functions. They allow us to reverse the effects of exponents, helping us solve problems that involve working backwards from a result.
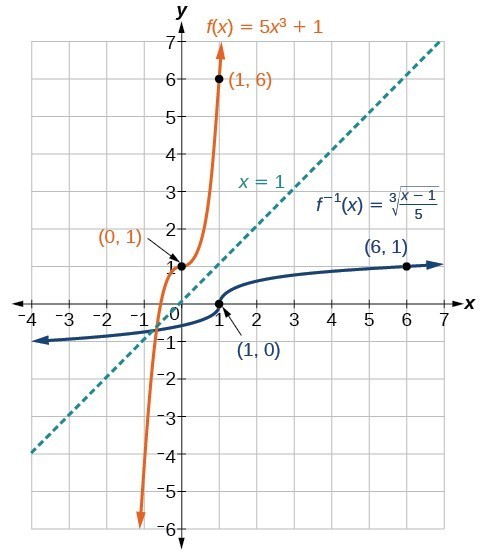
In our smartphone example, to find the light intensity for a given brightness, we need the inverse of our cubic function. This inverse turns out to be a radical function:
[latex]f^{-1}(x) = \sqrt[3]{\frac{x-1}{0.1}}[/latex]
This is a cube root function – a type of radical function that “undoes” the cube in our original polynomial.
radical functions
A radical function is a function that involves the use of a radical (root) symbol to indicate the root of a number or expression.
The general form of a radical function is
[latex]f(x) = \sqrt[n]{g(x)}[/latex]
where:
- [latex]\sqrt[n]{\cdot}[/latex] denotes the [latex]n[/latex]-th root.
- [latex]g(x)[/latex] is any function of [latex]x[/latex].
- [latex]n[/latex] is a positive integer indicating the degree of the root.
- Square Root Function:
- When [latex]n = 2[/latex], the function is called a square root function. The radical symbol [latex]\sqrt{\cdot}[/latex] is used without explicitly writing the [latex]2[/latex], known as the “phantom” [latex]2[/latex]. Thus, It is written as [latex]f(x) = \sqrt{x}[/latex].
- Cube Root Function:
- When [latex]n = 3[/latex], the function is called a cube root function. It is written as [latex]f(x) = \sqrt[3]{x}[/latex].
- Higher-Order Root Functions:
- For [latex]n \ge 3[/latex], the function represents higher-order roots, such as fourth roots, fifth roots, etc.
While it is not possible to find an inverse function of most polynomial functions, some basic polynomials do have inverses that are functions. Such functions are called invertible functions, and we use the notation [latex]{f}^{-1}\left(x\right)[/latex].
An important relationship between inverse functions is that they “undo” each other. If [latex]{f}^{-1}[/latex] is the inverse of a function [latex]f[/latex], then [latex]f[/latex] is the inverse of the function [latex]{f}^{-1}[/latex]. In other words, whatever the function [latex]f[/latex] does to [latex]x[/latex], [latex]{f}^{-1}[/latex] undoes it—and vice-versa. More formally, we write
[latex]{f}^{-1}\left(f\left(x\right)\right)=x,\text{for all }x\text{ in the domain of }f[/latex]
and
[latex]f\left({f}^{-1}\left(x\right)\right)=x,\text{for all }x\text{ in the domain of }{f}^{-1}[/latex]
- Verify that [latex]f[/latex] is a one-to-one function.
- Replace [latex]f\left(x\right)[/latex] with [latex]y[/latex].
- Interchange [latex]x[/latex] and [latex]y[/latex].
- Solve for [latex]y[/latex], and rename the function [latex]{f}^{-1}\left(x\right)[/latex].