Using the Square Root Property
When there is no linear term in the equation, another method of solving a quadratic equation is by using the square root property, in which we isolate the [latex]{x}^{2}[/latex] term and take the square root of the number on the other side of the equal sign. Keep in mind that sometimes we may have to manipulate the equation to isolate the [latex]{x}^{2}[/latex] term so that the square root property can be used.
square root property
With the [latex]{x}^{2}[/latex] term isolated, the square root property states that:
where [latex]k[/latex] is a non-negative real number.
- Isolate the [latex]{x}^{2}[/latex] term on one side of the equal sign.
- Take the square root of both sides of the equation, putting a [latex]\pm[/latex] sign before the expression on the side opposite the squared term.
- Simplify the numbers on the side with the [latex]\pm[/latex] sign.
[latex]\begin{align*} \text{Given equation:} & \quad x^2 = 8 \\ \text{Apply the square root property:} & \quad x = \pm \sqrt{8} \\ \text{Simplify the square root:} & \quad \sqrt{8} = \sqrt{4 \times 2} = 2\sqrt{2} \\ \text{Thus, the solution is:} & \quad x = \pm 2\sqrt{2} \end{align*}[/latex]
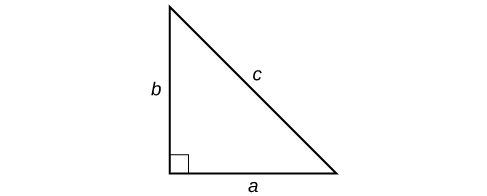
Using the Pythagorean Theorem
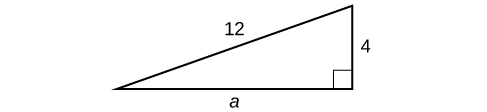
One of the most famous formulas in mathematics is the Pythagorean Theorem. It is based on a right triangle and states the relationship among the lengths of the sides as [latex]{a}^{2}+{b}^{2}={c}^{2}[/latex], where [latex]a[/latex] and [latex]b[/latex] refer to the legs of a right triangle adjacent to the [latex]90^\circ[/latex] angle, and [latex]c[/latex] refers to the hypotenuse. It has immeasurable uses in architecture, engineering, the sciences, geometry, trigonometry, and algebra, and in everyday applications.
We use the Pythagorean Theorem to solve for the length of one side of a triangle when we have the lengths of the other two. Because each of the terms is squared in the theorem, when we are solving for a side of a triangle, we have a quadratic equation. We can use the methods for solving quadratic equations that we learned in this section to solve for the missing side.
The Pythagorean Theorem is given as
where [latex]a[/latex] and [latex]b[/latex] refer to the legs of a right triangle adjacent to the [latex]{90}^{\circ }[/latex] angle, and [latex]c[/latex] refers to the hypotenuse.