Polynomial Basics

For the following exercises, identify the degree of the polynomial.

1. [latex]7x - 2x^2 + 13[/latex]
2. [latex]-625a^8 + 16b^4[/latex]
3. [latex]x^2 + 4x + 4[/latex]

For the following exercises, find the sum or difference.

4. [latex](12x^2 + 3x) - (8x^2 - 19)[/latex]
5. [latex](6w^2 + 24w + 24) - (3w^2 - 6w + 3)[/latex]
6. [latex](11b^4 - 6b^3 + 18b^2 - 4b + 8) - (3b^3 + 6b^2 + 3b)[/latex]

For the following exercises, find the product.

7. [latex](4x + 2)(6x - 4)[/latex]
8. [latex](6b^2 - 6)(4b^2 - 4)[/latex]
9. [latex](9v - 11)(11v - 9)[/latex]
10. [latex](8n - 4)(n^2 + 9)[/latex]

For the following exercises, expand the binomial.

11. [latex](3y - 7)^2[/latex]
12. [latex](4p + 9)^2[/latex]
13. [latex](3y - 6)^2[/latex]

For the following exercises, multiply the binomials.

14. [latex](4c + 1)(4c - 1)[/latex]
15. [latex](15n - 6)(15n + 6)[/latex]
16. [latex](4 + 4m)(4 - 4m)[/latex]
17. [latex](11q - 10)(11q + 10)[/latex]

For the following exercises, multiply the polynomials.

18. [latex](4t^2 + t - 7)(4t^2 - 1)[/latex]
19. [latex](y-2)(y^2 - 4y -9)[/latex]
20. [latex](3p^2 + 2p - 10)(p - 1)[/latex]
21. [latex](a+b)(a-b)[/latex]
22. [latex](4t - 5u)^2[/latex]
23. [latex](4t - x)(t - x + 1)[/latex]
24. [latex](4r - d)(6r + 7d)[/latex]

Factoring Polynomials

For the following exercises, find the greatest common factor.

1. [latex]49mb^2 - 35m^2ba + 77ma^2[/latex]
2. [latex]200p^3m^3 - 30p^2m^3 + 40m^3[/latex]
3. [latex]6y^4 - 2y^3 + 3y^2 - y[/latex]

For the following exercises, factor by grouping.

4. [latex]2a^2 + 9a - 18[/latex]
5. [latex]6n^2 - 19n - 11[/latex]
6. [latex]2p^2 - 5p - 7[/latex]

For the following exercises, factor the polynomial.

7. [latex]10h^2 - 9h - 9[/latex]
8. [latex]9d^2 - 73d + 8[/latex]
9. [latex]12t^2 + t - 13[/latex]
10. [latex]16x^2 - 100[/latex]
11. [latex]121p^2 - 169[/latex]
12. [latex]361d^2 - 81[/latex]
13. [latex]144b^2 - 25c^2[/latex]
14. [latex]49n^2 + 168n + 144[/latex]
15. [latex]225y^2 + 120y + 16[/latex]
16. [latex]25p^2 - 120p + 144[/latex]

For the following exercises, factor the polynomials.

17. [latex]x^3 + 216[/latex]
18. [latex]125a^3 + 343[/latex]
19. [latex]64x^3 - 125[/latex]
20. [latex]125r^3 + 1,728s^3[/latex]
21. [latex]3c(2c + 3)^{-\dfrac{1}{4}} - 5(2c + 3)^{\dfrac{3}{4}}[/latex]
22. [latex]14x(x + 2)^{-\dfrac{2}{5}} + 5(x + 2)^{\dfrac{3}{5}}[/latex]
23. [latex]5z(2z - 9)^{-\dfrac{3}{2}} + 11(2z - 9)^{-\dfrac{1}{2}}[/latex]

For the following exercises, consider this scenario:

Charlotte has appointed a chairperson to lead a city beautification project. The first act is to install statues and fountains in one of the city’s parks. The park is a rectangle with an area of [latex]98x^2 + 105x − 27m^2[/latex], as shown in the figure below. The length and width of the park are perfect factors of the area.

24. Factor by grouping to find the length and width of the park.
25. A statue is to be placed in the center of the park. The area of the base of the statue is [latex]4x^2 + 12x + 9 m^2[/latex]. Factor the area to find the lengths of the sides of the statue.
26. At the northwest corner of the park, the city is going to install a fountain. The area of the base of the fountain is [latex]9x^2 − 25 m^2[/latex]. Factor the area to find the lengths of the sides of the fountain.

Rational Expressions

For the following exercises, simplify the rational expressions.

1. [latex]\dfrac{y^2 + 10y + 25}{y^2 + 11y + 30}[/latex]
2. [latex]\dfrac{9b^2 + 18b + 9}{3b + 3}[/latex]
3. [latex]\dfrac{2x^2 + 7x - 4}{4x^2 + 2x - 2}[/latex]
4. [latex]\dfrac{a^2 + 9a + 18}{a^2 + 3a - 18}[/latex]
5. [latex]\dfrac{12n^2 - 29n - 8}{28n^2 - 5n - 3}[/latex]

For the following exercises, multiply the rational expressions and express the product in simplest form.

6. [latex]\dfrac{c^2 + 2c - 24}{c^2 + 12c + 36} \cdot \dfrac{c^2 - 10c + 24}{c^2 - 8c + 16}[/latex]
7. [latex]\dfrac{10h^2 - 9h - 9}{2h^2 - 19h + 24} \cdot \dfrac{h^2 - 16h + 64}{5h^2 - 37h + 72}[/latex]
8. [latex]\dfrac{2d^2 + 15d + 25}{4d^2 - 25} \cdot \dfrac{2d^2 - 15d + 25}{25d^2 - 1}[/latex]
9. [latex]\dfrac{t^2 - 1}{t^2 + 4t + 3} \cdot \dfrac{t^2 + 2t - 15}{t^2 - 4t + 3}[/latex]
10. [latex]\dfrac{36x^2 - 25}{6x^2 + 65x + 50} \cdot \dfrac{3x^2 + 32x + 20}{18x^2 + 27x + 10}[/latex]

For the following exercises, divide the rational expressions.

11. [latex]\dfrac{6p^2 + p - 12}{8p^2 + 18p + 9} \div \dfrac{6p^2 - 11p + 4}{2p^2 + 11p - 6}[/latex]
12. [latex]\dfrac{18d^2 + 77d - 18}{27d^2 - 15d + 2} \div \dfrac{3d^2 + 29d - 44}{9d^2 - 15d + 4}[/latex]
13. [latex]\dfrac{144b^2 - 25}{72b^2 - 6b - 10} \div \dfrac{18b^2 - 21b + 5}{36b^2 - 18b - 10}[/latex]
14. [latex]\dfrac{22y^2 + 59y + 10}{12y^2 + 28y - 5} \div \dfrac{11y^2 + 46y + 8}{24y^2 - 10y + 1}[/latex]

For the following exercises, add and subtract the rational expressions, and then simplify.

15. [latex]\dfrac{4}{x} + \dfrac{10}{y}[/latex]
16. [latex]\dfrac{4}{a + 1} + \dfrac{5}{a - 3}[/latex]
17. [latex]\dfrac{y + 3}{y - 2} + \dfrac{y - 3}{y + 1}[/latex]
18. [latex]\dfrac{3z}{z + 1} + \dfrac{2z + 5}{z - 2}[/latex]
19. [latex]\dfrac{x}{x + 1} + \dfrac{y}{y + 1}[/latex]

For the following exercises, simplify the rational expression.

20. [latex]\dfrac{\dfrac{2}{a} + \dfrac{7}{b}}{b}[/latex]
21. [latex]\dfrac{\dfrac{3}{a} + \dfrac{b}{6}}{\dfrac{2b}{3a}}[/latex]
22. [latex]\dfrac{\dfrac{a}{b} - \dfrac{b}{a}}{ab}[/latex]
23. [latex]\dfrac{\dfrac{2c}{c + 2} + \dfrac{c - 1}{c + 1}}{\dfrac{2c + 1}{c + 1}}[/latex]

24. Brenda is placing tile on her bathroom floor. The area of the floor is [latex]15x^2 - 8x - 7 \, \text{ft}^2[/latex]. The area of one tile is [latex]x^2 - 2x + 1 \, \text{ft}^2[/latex]. To find the number of tiles needed, simplify the rational expression: [latex]\dfrac{15x^2 - 8x - 7}{x^2 - 2x + 1}[/latex].
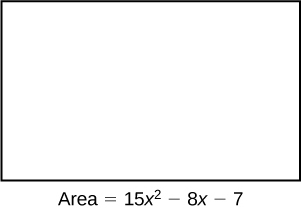
25. Elroi wants to mulch his garden. His garden is [latex]x^2 + 18x + 81 \, \text{ft}^2[/latex]. One bag of mulch covers [latex]x^2 - 81 \, \text{ft}^2[/latex]. Divide the expressions and simplify to find how many bags of mulch Elroi needs to mulch his garden.