• Draw parabolas on a graph, understanding how their shapes change based on whether their vertex is at the origin or another point
• Write equations of parabolas in standard form
• Solve applied problems involving parabolas

Solving Applied Problems Involving Parabolas

As we mentioned at the beginning of the section, parabolas are used to design many objects we use every day, such as telescopes, suspension bridges, microphones, and radar equipment. Parabolic mirrors, such as the one used to light the Olympic torch, have a very unique reflecting property.

Did you know that the Olympic torch is lit several months before the start of the games? The ceremonial method for lighting the flame is the same as in ancient times. The ceremony takes place at the Temple of Hera in Olympia, Greece, and is rooted in Greek mythology, paying tribute to Prometheus, who stole fire from Zeus to give to all humans. One of eleven acting priestesses places the torch at the focus of a parabolic mirror, which focuses light rays from the sun to ignite the flame.

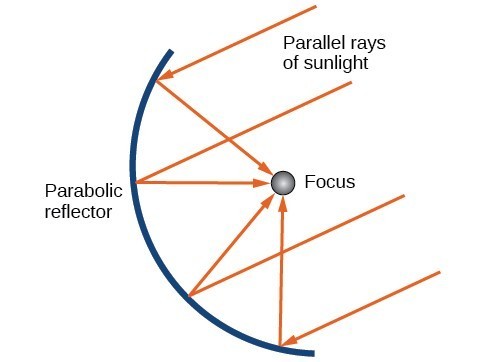
When rays of light parallel to the parabola’s axis of symmetry are directed toward any surface of the mirror, the light is reflected directly to the focus. This is why the Olympic torch is ignited when it is held at the focus of the parabolic mirror.

Parabolic mirrors have the ability to focus the sun’s energy to a single point, raising the temperature hundreds of degrees in a matter of seconds. Thus parabolic mirrors are featured in many low-cost, energy efficient solar products, such as solar cookers, solar heaters, and even travel-sized fire starters.

 

A cross-section of a design for a travel-sized solar fire starter. The sun’s rays reflect off the parabolic mirror toward an object attached to the igniter. Because the igniter is located at the focus of the parabola, the reflected rays cause the object to burn in just seconds.

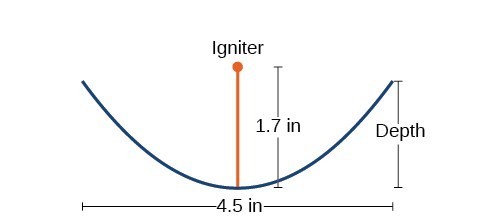
1. Find the equation of the parabola that models the fire starter. Assume that the vertex of the parabolic mirror is the origin of the coordinate plane.
2. Use the equation found in part (a) to find the depth of the fire starter.

Show Solution

 

The vertex of the dish is the origin of the coordinate plane, so the parabola will take the standard form [latex]{x}^{2}=4py[/latex], where [latex]p>0[/latex]. The igniter, which is the focus, is 1.7 inches above the vertex of the dish. Thus we have [latex]p=1.7[/latex].

[latex]\begin{align}&{x}^{2}=4py && \text{Standard form of upward-facing parabola with vertex (0,0)} \\ &{x}^{2}=4\left(1.7\right)y && \text{Substitute 1}\text{.7 for }p. \\ &{x}^{2}=6.8y && \text{Multiply}. \end{align}[/latex]

The dish extends [latex]\frac{4.5}{2}=2.25[/latex] inches on either side of the origin. We can substitute 2.25 for [latex]x[/latex] in the equation from part (a) to find the depth of the dish.

[latex]\begin{align}&{x}^{2}=6.8y && \text{Equation found in part (a)}. \\ &{\left(2.25\right)}^{2}=6.8y && \text{Substitute 2}\text{.25 for }x. \\ &y\approx 0.74 && \text{Solve for }y. \end{align}[/latex]

The dish is about [latex]0.74[/latex] inches deep.

Solar cookers have become an innovative solution for sustainable cooking in many parts of the world, particularly in regions with abundant sunlight. These devices harness solar energy to prepare food, reducing reliance on traditional fuels and decreasing environmental impact.Let’s consider a specific design of a parabolic solar cooker:

The top of the dish-shaped reflector has a diameter of [latex]1600[/latex] mm. The sun’s rays reflect off the parabolic mirror toward the “cooker” (the focal point where food is placed for cooking), which is positioned [latex]320[/latex] mm from the base of the parabola.

1. Find an equation that models a cross-section of the solar cooker. Assume that the vertex of the parabolic mirror is the origin of the coordinate plane, and that the parabola opens to the right (i.e., has the [latex]x[/latex]-axis as its axis of symmetry).
2. Use the equation found in part (a) to find the depth of the cooker.

Show Solution

1. [latex]{y}^{2}=1280x[/latex]
2. The depth of the cooker is 500 mm