- Solve equations that include fractions with variables.
- Solve equations with roots and fractional powers.
- Use factoring to find solutions to polynomial equations.
- Find solutions to equations that involve absolute values.
- Find solutions to inequalities that involve absolute values.
Solving a Rational Equation
The Main Idea
- Definition of Rational Equations:
- Contains at least one rational expression
- Variable appears in at least one denominator
- Solving Process:
- Factor all denominators
- Find and exclude values that make denominators zero
- Determine the Least Common Denominator (LCD)
- Multiply both sides by the LCD
- Solve the resulting equation
- Check solutions in the original equation
- Cross-Multiplication Method:
- For equations in the form [latex]\frac{a}{b} = \frac{c}{d}[/latex]
- Multiply to get [latex]ad = bc[/latex]
- Handling Binomial Denominators:
- Treat binomials (e.g., [latex]x + 1[/latex]) as single units
- Factor completely before finding LCD
- Importance in Algebra:
- Bridge between linear equations and more complex algebraic structures
- Foundation for solving many real-world problems
[latex]\dfrac{2}{3x} = \dfrac{1}{4} - \dfrac{1}{6x}[/latex]
[latex]-\dfrac{5}{2x} + \dfrac{3}{4x} = -\dfrac{7}{4}[/latex]
You can view the transcript for “Ex 2: Solving Rational Equations” here (opens in new window).
Radical Equations
The Main Idea
- Definition:
- Equations containing variables under a radical symbol
- Example: [latex]\sqrt{3x + 18} = x[/latex]
- Solving Process:
- Isolate the radical term
- Raise both sides to the power of the radical’s index
- Solve the resulting equation
- Check for extraneous solutions
- Extraneous Solutions:
- Solutions that satisfy the altered equation but not the original
- Result from squaring or cubing both sides
- Must be checked by substitution in the original equation
- Multiple Radicals:
- Isolate one radical at a time
- Repeat the process for each radical
Problem-Solving Strategy
- Identify all radical terms
- Plan the isolation sequence for multiple radicals
- Raise both sides to appropriate powers
- Solve the resulting polynomial equation
- Check all solutions in the original equation
You can view the transcript for “Ex 3: Solve Radical Equations – Square Roots” here (opens in new window).
Solve Equations With Rational Exponents
The Main Idea
- Rational Exponents:
- Fractions as exponents
- Notation: [latex]a^{\frac{m}{n}} = \sqrt[n]{a^m}[/latex]
- Equivalence to Radicals:
- [latex]a^{\frac{1}{n}} = \sqrt[n]{a}[/latex]
- [latex]a^{\frac{m}{n}} = (\sqrt[n]{a})^m[/latex]
- Solving Strategy:
- Raise both sides to the reciprocal power
- Simplify using exponent rules
- Solve the resulting equation
- Key Exponent Rules:
- Product: [latex]a^m \cdot a^n = a^{m+n}[/latex]
- Quotient: [latex]\frac{a^m}{a^n} = a^{m-n}[/latex]
- Power: [latex]{\left({a}^{m}\right)}^{n}={a}^{m\cdot n}[/latex]
Problem-Solving Technique
- Identify the rational exponent
- Determine its reciprocal
- Apply the reciprocal exponent to both sides
- Simplify using exponent rules
- Solve the resulting equation
- Check the solution
You can view the transcript for “Solve Equations with Rational Exponents (Two Solutions)” here (opens in new window).
Polynomial Equations
The Main Idea
- Definition: A polynomial equation is an equation of the form: [latex]a_nx^n + a_{n-1}x^{n-1} + \ldots + a_2x^2 + a_1x + a_0 = 0[/latex] where [latex]n[/latex] is a positive integer and [latex]a_n \neq 0[/latex]
- Degree:
- The highest power of the variable in the polynomial
- Determines the maximum number of solutions
- Zero-Product Property: If [latex]ab = 0[/latex], then [latex]a = 0[/latex] or [latex]b = 0[/latex]
- Fundamental to solving polynomial equations by factoring
- Solution Types:
- Real solutions (rational or irrational)
- Complex solutions (when real solutions don’t exist)
Problem-Solving Steps
- Arrange the polynomial in standard form (descending powers)
- Factor out the greatest common factor (GCF)
- Look for special patterns or grouping opportunities
- Factor completely
- Apply the zero-product property
- Solve the resulting linear equations
- Check solutions in the original equation
[latex]2x^4 - 18x^2 + 40 = 0[/latex]
You can view the transcript for “Ex: Factor and Solve a Polynomial Equation” here (opens in new window).
Absolute Value Equations
The Main Idea
- Definition of Absolute Value:
- Represents the distance of a number from zero on the number line
- Always non-negative
- Formally defined as: [latex]|x| = \begin{cases} x & \text{if } x \geq 0 \\ -x & \text{if } x < 0 \end{cases}[/latex]
- Absolute Value Equation:
- An equation containing an absolute value expression
- General form: [latex]|A| = B[/latex], where A is an expression and B is a non-negative number
- Properties of Absolute Value Equations:
- If [latex]|A| = B[/latex], then [latex]A = B[/latex] or [latex]A = -B[/latex] when [latex]B \geq 0[/latex]
- If [latex]B < 0[/latex], the equation [latex]|A| = B[/latex] has no solution
- Standard Form of Linear Absolute Value Equations:
- [latex]|ax + b| = c[/latex], where [latex]a \neq 0[/latex] and [latex]c[/latex] is a real number
- Number of Solutions:
- If [latex]c < 0[/latex]: No solution
- If [latex]c = 0[/latex]: One solution
- If [latex]c > 0[/latex]: Two solutions
Solving Process:
- Isolate the absolute value expression on one side of the equation
- Consider two cases: positive and negative
- Solve each case as a linear equation
- Check solutions in the original equation
You can view the transcript for “Isolate binomial absolute value” here (opens in new window).
Absolute Value Inequalities
The Main Idea
- Definition of Absolute Value Inequalities:
- Equations of the form [latex]|A| < B[/latex], [latex]|A| \leq B[/latex], [latex]|A| > B[/latex], or [latex]|A| \geq B[/latex]
- [latex]A[/latex] and [latex]B[/latex] are algebraic expressions, often involving a variable [latex]x[/latex]
- Solving Absolute Value Inequalities:
- For [latex]|X| < k[/latex] (where [latex]k > 0[/latex]): Equivalent to [latex]-k < X < k[/latex]
- For [latex]|X| > k[/latex] (where [latex]k > 0[/latex]): Equivalent to [latex]X < -k[/latex] or [latex]X > k[/latex]
- Similar rules apply for [latex]\leq[/latex] and [latex]\geq[/latex]
- Graphical Interpretation:
- Solutions represent intervals on a number line
- [latex]|X| < k[/latex]: Points within [latex]k[/latex] units of zero
- [latex]|X| > k[/latex]: Points more than [latex]k[/latex] units away from zero
Try It
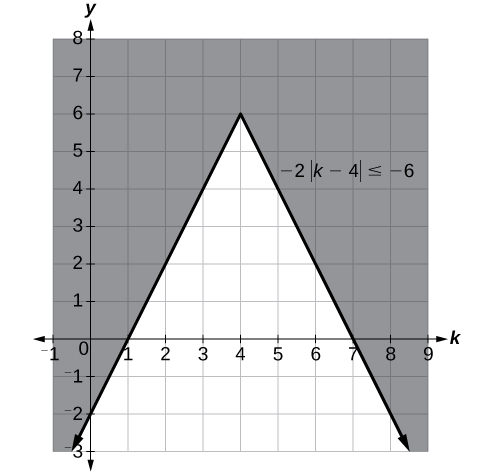
Solve [latex]-2|k - 4|\le -6[/latex].
You can view the transcript for “Absolute Value Inequality” here (opens in new window).