- Determine whether a function is one-to-one
Determining Whether a Function is One-to-One
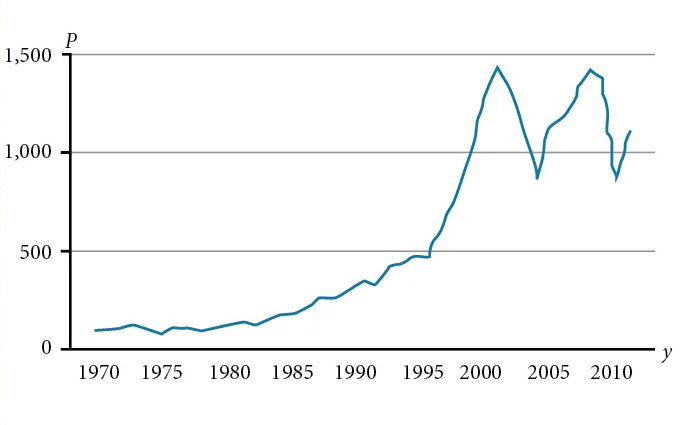
Some functions have a given output value that corresponds to two or more input values. For example, in the stock chart shown below, the stock price was [latex]$1000[/latex] on five different dates, meaning that there were five different input values that all resulted in the same output value of [latex]$1000[/latex].
However, some functions have only one input value for each output value, as well as having only one output for each input. We call these functions one-to-one functions. As an example, consider a school that uses only letter grades and decimal equivalents, as listed in the table below.
| Letter grade | Grade point average |
|---|---|
| A | 4.0 |
| B | 3.0 |
| C | 2.0 |
| D | 1.0 |
This grading system represents a one-to-one function, because each letter input yields one particular grade point average output and each grade point average corresponds to one input letter.
one-to-one function
A one-to-one function is a function in which each output value corresponds to exactly one input value.
- Is a balance a one-to-one function of the bank account number?
- Is a bank account number a one-to-one function of the balance?
- Is a balance a one-to-one function of the bank account number?
The Horizontal Line Test
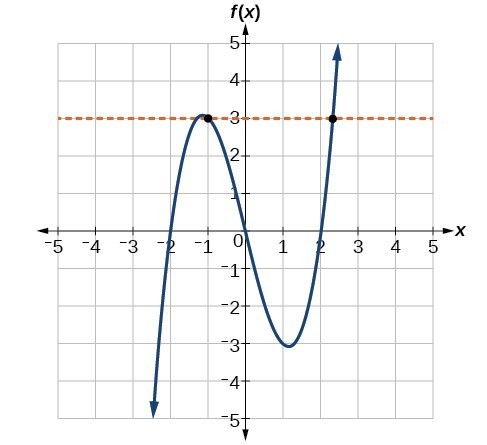
Once we have determined that a graph defines a function, an easy way to determine if it is a one-to-one function is to use the horizontal line test. Draw horizontal lines through the graph. If we can draw any horizontal line that intersects a graph more than once, then the graph does not represent a one-to-one function because that [latex]y[/latex] value has more than one input.
horizontal line test
The horizontal line test checks if a function is one-to-one by ensuring that no horizontal line intersects the graph more than once.
- Inspect the graph to see if any horizontal line drawn would intersect the curve more than once.
- If there is any such line, the function is not one-to-one.
- If no horizontal line can intersect the curve more than once, the function is one-to-one.