- Figure out which values make a rational expression impossible to calculate (like dividing by zero)
Rational Expressions and Undefined Values
A rational expression is an algebraic expression that can be written as the quotient of two polynomials, [latex]P(x)[/latex] and [latex]Q(x)[/latex], where [latex]Q(x) \neq 0[/latex]. It takes the general form:
[latex]\frac{P(x)}{Q(x)}[/latex]
where [latex]P(x)[/latex] is the numerator and [latex]Q(x)[/latex] is the denominator.
The domain of a rational expression includes all real numbers except those that make the denominator equal to zero. When the denominator equals zero, the expression is undefined. This concept is rooted in the fundamental principle that division by zero is impossible in mathematics.
rational expressions and undefined values
A rational expression is undefined when its denominator equals zero.
- Isolate the denominator.
- Set the denominator equal to zero.
- Solve the resulting equation.
The solutions to this equation are the values that make the rational expression undefined.
Determine the value(s) of [latex]x[/latex] for which the following rational expression is undefined:
[latex]\frac{x^2 - 4}{x - 2}[/latex]
Find the values of [latex]x[/latex] that make the following rational expression undefined:
[latex]\frac{x^2 + 3x}{x^2 - 4}[/latex]
Determine all values of [latex]x[/latex] for which the following rational expression is undefined:
[latex]\frac{2x^2 - 5}{x^3 - x}[/latex]
Undefined values in rational expressions correspond to vertical asymptotes in their graphs. As [latex]x[/latex] approaches an undefined value, the expression approaches infinity or negative infinity, creating a vertical line that the graph approaches but never crosses.
For example, in the graph of [latex]y = \frac{1}{x - 2}[/latex]:
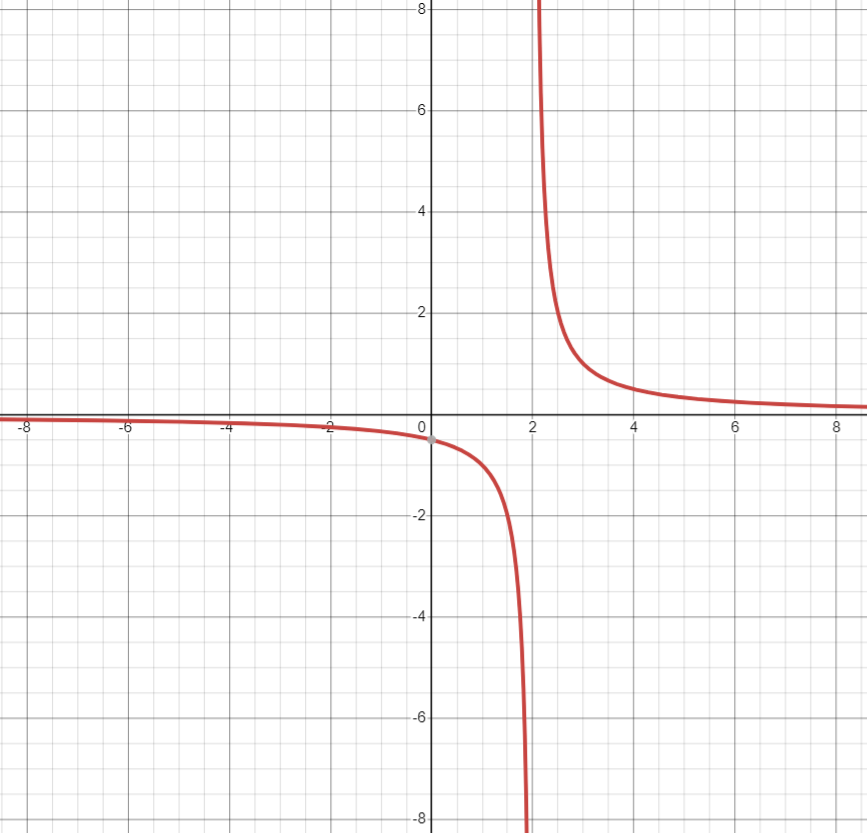
- As [latex]x[/latex] approaches [latex]2[/latex] from the left, [latex]y[/latex] approaches positive infinity.
- As [latex]x[/latex] approaches [latex]2[/latex] from the right, [latex]y[/latex] approaches negative infinity.
- The line [latex]x = 2[/latex] is a vertical asymptote of the graph.
Common Mistakes to Avoid
- Forgetting to check for undefined values before simplifying.
- Assuming only linear terms in the denominator can cause undefined values.
- Neglecting to factor completely when dealing with higher degree polynomials.
- Confusing zero values of the numerator with undefined values.
An indeterminate form occurs when a mathematical expression yields an ambiguous result. The form 0/0 is one such case.