Inverse Functions: Learn It 2

Giselle Miller

Inverse Functions: Learn It 2

Determine the Domain and Range of an Inverse Function

The outputs of the function [latex]f[/latex] are the inputs to [latex]{f}^{-1}[/latex], so the range of [latex]f[/latex] is also the domain of [latex]{f}^{-1}[/latex]. Likewise, because the inputs to [latex]f[/latex] are the outputs of [latex]{f}^{-1}[/latex], the domain of [latex]f[/latex] is the range of [latex]{f}^{-1}[/latex]. We can visualize the situation.

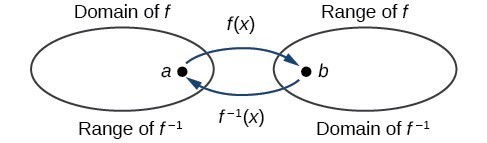
Domain and range of a function and its inverse. — Domain and range of a function and its inverse

domain and range of inverse functions

The range of a function [latex]f\left(x\right)[/latex] is the domain of the inverse function [latex]{f}^{-1}\left(x\right)[/latex].

The domain of [latex]f\left(x\right)[/latex] is the range of [latex]{f}^{-1}\left(x\right)[/latex].

When a function has no inverse function, it is possible to create a new function where that new function on a limited domain does have an inverse function.

For example, the inverse of [latex]f\left(x\right)=\sqrt{x}[/latex] is [latex]{f}^{-1}\left(x\right)={x}^{2}[/latex], because a square “undoes” a square root; but the square is only the inverse of the square root on the domain [latex]\left[0,\infty \right)[/latex], since that is the range of [latex]f\left(x\right)=\sqrt{x}[/latex].
[latex]\\[/latex]
We can look at this problem from the other side, starting with the square (toolkit quadratic) function [latex]f\left(x\right)={x}^{2}[/latex]. If we want to construct an inverse to this function, we run into a problem, because for every given output of the quadratic function, there are two corresponding inputs (except when the input is 0).

For example, the output [latex]9[/latex] from the quadratic function corresponds to the inputs [latex]3[/latex] and [latex]–3[/latex].

But an output from a function is an input to its inverse; if this inverse input corresponds to more than one inverse output (input of the original function), then the “inverse” is not a function at all!
[latex]\\[/latex]
To put it differently, the quadratic function is not a one-to-one function; it fails the horizontal line test, so it does not have an inverse function.

In order for a function to have an inverse, it must be a one-to-one function. In many cases, if a function is not one-to-one, we can still restrict the function to a part of its domain on which it is one-to-one.

We can make a restricted version of the square function [latex]f\left(x\right)={x}^{2}[/latex] with its range limited to [latex]\left[0,\infty \right)[/latex], which is a one-to-one function (it passes the horizontal line test) and which has an inverse (the square-root function).
[latex]\\[/latex]
If [latex]f\left(x\right)={\left(x - 1\right)}^{2}[/latex] on [latex]\left[1,\infty \right)[/latex], then the inverse function is [latex]{f}^{-1}\left(x\right)=\sqrt{x}+1[/latex].

The domain of [latex]f[/latex] = range of [latex]{f}^{-1}[/latex] = [latex]\left[1,\infty \right)[/latex].
The domain of [latex]{f}^{-1}[/latex] = range of [latex]f[/latex] = [latex]\left[0,\infty \right)[/latex].

Is it possible for a function to have more than one inverse?

No. If two supposedly different functions, say, [latex]g[/latex] and [latex]h[/latex], both meet the definition of being inverses of another function [latex]f[/latex], then you can prove that [latex]g=h[/latex]. We have just seen that some functions only have inverse functions if we restrict the domain of the original function. In these cases, there may be more than one way to restrict the domain, leading to different inverse functions. However, on any one domain, the original function still has only one unique inverse function.

How To: Given a function, find the domain and range of its inverse.

If the function is one-to-one, write the range of the original function as the domain of the inverse, and write the domain of the original function as the range of the inverse.
If the domain of the original function needs to be restricted to make it one-to-one, then this restricted domain becomes the range of the inverse function.

Identify which of the toolkit functions besides the quadratic function are not one-to-one, and find a restricted domain on which each function is one-to-one, if any. We restrict the domain in such a fashion that the function assumes all [latex]y[/latex]-values exactly once.
[latex]\\[/latex]
Fora refresher of the tool kit functions, expand the review below.

Constant	Identity	Quadratic	Cubic	Reciprocal
[latex]f\left(x\right)=c[/latex]	[latex]f\left(x\right)=x[/latex]	[latex]f\left(x\right)={x}^{2}[/latex]	[latex]f\left(x\right)={x}^{3}[/latex]	[latex]f\left(x\right)=\frac{1}{x}[/latex]
Reciprocal squared	Cube root	Square root	Absolute value
[latex]f\left(x\right)=\frac{1}{{x}^{2}}[/latex]	[latex]f\left(x\right)=\sqrt[3]{x}[/latex]	[latex]f\left(x\right)=\sqrt{x}[/latex]	[latex]f\left(x\right)=\|x\|[/latex]