- Understand how to add and subtract matrices
- Figure out how to multiply a matrix by a number (scalar) to change its scale
- Learn to multiply two matrices together to find a new matrix
Matrices
Two club soccer teams, the Wildcats and the Mud Cats, are hoping to obtain new equipment for an upcoming season. The table shows the needs of both teams.
| Wildcats | Mud Cats | |
|---|---|---|
| Goals | [latex]6[/latex] | [latex]10[/latex] |
| Balls | [latex]30[/latex] | [latex]24[/latex] |
| Jerseys | [latex]14[/latex] | [latex]20[/latex] |
A goal costs [latex]$300[/latex]; a ball costs [latex]$10[/latex]; and a jersey costs [latex]$30[/latex]. How can we find the total cost for the equipment needed for each team?
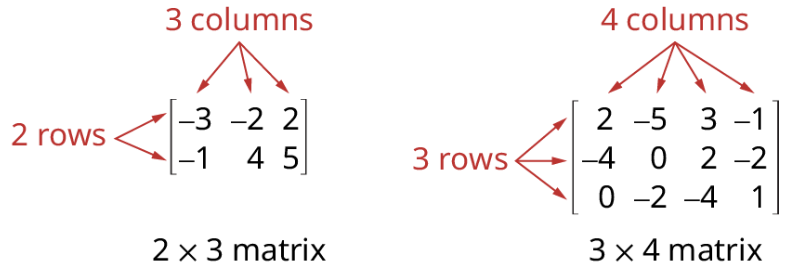
To solve a problem like this, we can use a matrix, which is a rectangular array of numbers. A row in a matrix is a set of numbers that are aligned horizontally. A column in a matrix is a set of numbers that are aligned vertically. Each number is an entry, sometimes called an element, of the matrix. Matrices (plural) are enclosed in [ ] or ( ) and are usually named with capital letters.
[latex]A=\left[\begin{array}{cc}1& 2\\ 3& 4\end{array}\right],B=\left[\begin{array}{ccc}\hfill 1& \hfill 2& \hfill 7\\ \hfill 0& \hfill -5& \hfill 6\\ \hfill 7& \hfill 8& \hfill 2\end{array}\right],C=\left[\begin{array}{c}\hfill -1\\ \hfill 0\\ \hfill 3\end{array}\begin{array}{c}3\\ 2\\ 1\end{array}\right][/latex]
A matrix is often referred to by its size or dimensions: [latex]\text{ }m\text{ }\times \text{ }n\text{ }[/latex] indicating [latex]m[/latex] rows and [latex]n[/latex] columns. Matrix entries are defined first by row and then by column.
[latex]A=\left[\begin{array}{ccc}{a}_{11}& {a}_{12}& {a}_{13}\\ {a}_{21}& {a}_{22}& {a}_{23}\\ {a}_{31}& {a}_{32}& {a}_{33}\end{array}\right][/latex]
matrix
A matrix is a rectangular array of numbers arranged in rows and columns.
A matrix with [latex]m[/latex] rows and [latex]n[/latex] columns has dimension [latex]m \times n[/latex].
Each number in the matrix is called an element or entry in the matrix.
Type of Matrices
- A square matrix is a matrix with dimensions [latex]\text{ }n\text{ }\times \text{ }n,\text{}[/latex] meaning that it has the same number of rows as columns:
[latex]A=\left[\begin{array}{ccc}{a}_{11}& {a}_{12}& {a}_{13}\\ {a}_{21}& {a}_{22}& {a}_{23}\\ {a}_{31}& {a}_{32}& {a}_{33}\end{array}\right][/latex]
- A row matrix is a matrix consisting of one row with dimensions [latex]1\text{ }\times \text{ }n[/latex]:
[latex]\left[\begin{array}{ccc}{a}_{11}& {a}_{12}& {a}_{13}\end{array}\right][/latex]
- A column matrix is a matrix consisting of one column with dimensions [latex]m\text{ }\times \text{ }1[/latex]:
[latex]\left[\begin{array}{c}{a}_{11}\\ {a}_{21}\\ {a}_{31}\end{array}\right][/latex]
- What are the dimensions of matrix [latex]A?[/latex]
- What are the entries at [latex]{a}_{31}[/latex] and [latex]{a}_{22}?[/latex]
[latex]A=\left[\begin{array}{rrrr}\hfill 2& \hfill & \hfill 1& \hfill 0\\ \hfill 2& \hfill & \hfill 4& \hfill 7\\ \hfill 3& \hfill & \hfill 1& \hfill -2\end{array}\right][/latex]