Standard Form of the Equation of a Hyperbola Centered at the Origin
The standard form of an equation of a hyperbola centered at the origin with vertices [latex]\left(\pm a,0\right)[/latex] and co-vertices [latex]\left(0\pm b\right)[/latex] is [latex]\dfrac{{x}^{2}}{{a}^{2}}-\dfrac{{y}^{2}}{{b}^{2}}=1[/latex].
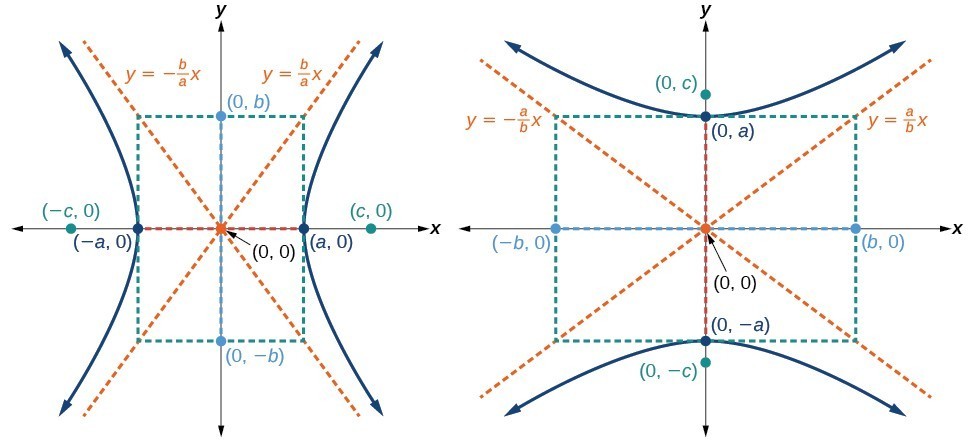
standard forms of the equation of a hyperbola with center [latex](0,0)[/latex]
The standard form of the equation of a hyperbola with center [latex]\left(0,0\right)[/latex] and transverse axis on the [latex]x[/latex]-axis is
[latex]\dfrac{{x}^{2}}{{a}^{2}}-\dfrac{{y}^{2}}{{b}^{2}}=1[/latex]
where
- the length of the transverse axis is [latex]2a[/latex]
- the coordinates of the vertices are [latex]\left(\pm a,0\right)[/latex]
- the length of the conjugate axis is [latex]2b[/latex]
- the coordinates of the co-vertices are [latex]\left(0,\pm b\right)[/latex]
- the distance between the foci is [latex]2c[/latex], where [latex]{c}^{2}={a}^{2}+{b}^{2}[/latex]
- the coordinates of the foci are [latex]\left(\pm c,0\right)[/latex]
- the equations of the asymptotes are [latex]y=\pm \dfrac{b}{a}x[/latex]
The standard form of the equation of a hyperbola with center [latex]\left(0,0\right)[/latex] and transverse axis on the [latex]y[/latex]-axis is
[latex]\dfrac{{y}^{2}}{{a}^{2}}-\dfrac{{x}^{2}}{{b}^{2}}=1[/latex]
where
- the length of the transverse axis is [latex]2a[/latex]
- the coordinates of the vertices are [latex]\left(0,\pm a\right)[/latex]
- the length of the conjugate axis is [latex]2b[/latex]
- the coordinates of the co-vertices are [latex]\left(\pm b,0\right)[/latex]
- the distance between the foci is [latex]2c[/latex], where [latex]{c}^{2}={a}^{2}+{b}^{2}[/latex]
- the coordinates of the foci are [latex]\left(0,\pm c\right)[/latex]
- the equations of the asymptotes are [latex]y=\pm \dfrac{a}{b}x[/latex]
Note that the vertices, co-vertices, and foci are related by the equation [latex]{c}^{2}={a}^{2}+{b}^{2}[/latex]. When we are given the equation of a hyperbola, we can use this relationship to identify its vertices and foci.
- Determine whether the transverse axis lies on the [latex]x[/latex]– or [latex]y[/latex]-axis. Notice that [latex]{a}^{2}[/latex] is always under the variable with the positive coefficient. So, if you set the other variable equal to zero, you can easily find the intercepts. In the case where the hyperbola is centered at the origin, the intercepts coincide with the vertices.
- If the equation has the form [latex]\dfrac{{x}^{2}}{{a}^{2}}-\dfrac{{y}^{2}}{{b}^{2}}=1[/latex], then the transverse axis lies on the [latex]x[/latex]-axis. The vertices are located at [latex]\left(\pm a,0\right)[/latex], and the foci are located at [latex]\left(\pm c,0\right)[/latex].
- If the equation has the form [latex]\dfrac{{y}^{2}}{{a}^{2}}-\dfrac{{x}^{2}}{{b}^{2}}=1[/latex], then the transverse axis lies on the [latex]y[/latex]-axis. The vertices are located at [latex]\left(0,\pm a\right)[/latex], and the foci are located at [latex]\left(0,\pm c\right)[/latex].
- Solve for [latex]a[/latex] using the equation [latex]a=\sqrt{{a}^{2}}[/latex].
- Solve for [latex]c[/latex] using the equation [latex]c=\sqrt{{a}^{2}+{b}^{2}}[/latex].
Writing Equations of Hyperbolas Centered at the Origin
Just as with ellipses, writing the equation for a hyperbola in standard form allows us to calculate the key features: its center, vertices, co-vertices, foci, asymptotes, and the lengths and positions of the transverse and conjugate axes. Conversely, an equation for a hyperbola can be found given its key features. We begin by finding standard equations for hyperbolas centered at the origin.
Reviewing the standard forms given for hyperbolas centered at [latex]\left(0,0\right)[/latex], we see that the vertices, co-vertices, and foci are related by the equation [latex]{c}^{2}={a}^{2}+{b}^{2}[/latex]. Note that this equation can also be rewritten as [latex]{b}^{2}={c}^{2}-{a}^{2}[/latex]. This relationship is used to write the equation for a hyperbola when given the coordinates of its foci and vertices.
- Determine whether the transverse axis lies on the [latex]x[/latex]– or [latex]y[/latex]-axis.
- If the given coordinates of the vertices and foci have the form [latex]\left(\pm a,0\right)[/latex] and [latex]\left(\pm c,0\right)[/latex], respectively, then the transverse axis is the [latex]x[/latex]-axis. Use the standard form [latex]\dfrac{{x}^{2}}{{a}^{2}}-\dfrac{{y}^{2}}{{b}^{2}}=1[/latex].
- If the given coordinates of the vertices and foci have the form [latex]\left(0,\pm a\right)[/latex] and [latex]\left(0,\pm c\right)[/latex], respectively, then the transverse axis is the [latex]y[/latex]-axis. Use the standard form [latex]\dfrac{{y}^{2}}{{a}^{2}}-\dfrac{{x}^{2}}{{b}^{2}}=1[/latex].
- Find [latex]{b}^{2}[/latex] using the equation [latex]{b}^{2}={c}^{2}-{a}^{2}[/latex].
- Substitute the values for [latex]{a}^{2}[/latex] and [latex]{b}^{2}[/latex] into the standard form of the equation determined in Step 1.
