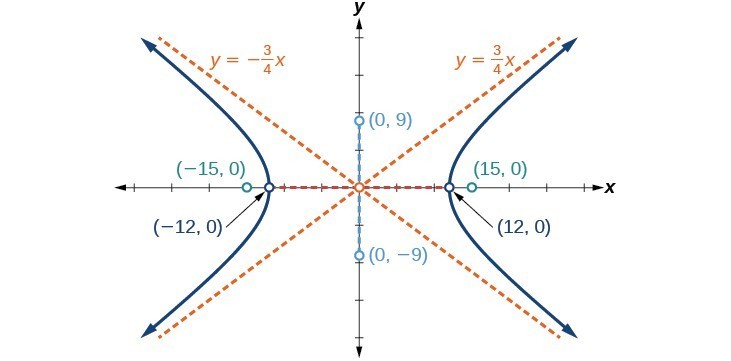
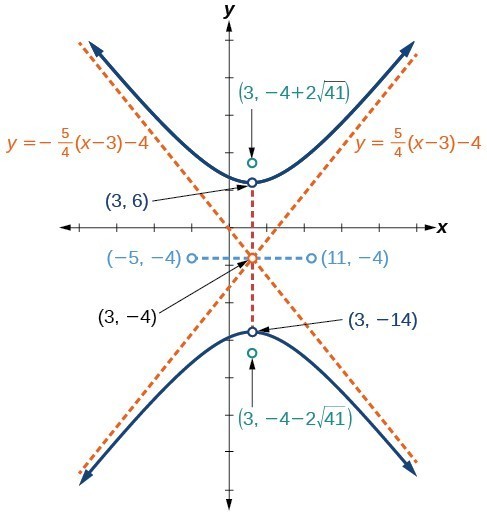
- Identify the key points of a hyperbola, including where it turns and its focus points
- Write equations of hyperbolas in standard form
- Draw hyperbolas on a graph, noting how their position and orientation change based on their center
- Solve applied problems involving hyperbolas
Hyperbolas
A hyperbola is the set of all points [latex]\left(x,y\right)[/latex] in a plane such that the difference of the distances between [latex]\left(x,y\right)[/latex] and the foci is a positive constant.
Notice that the definition of a hyperbola is very similar to that of an ellipse. The distinction is that the hyperbola is defined in terms of the difference of two distances, whereas the ellipse is defined in terms of the sum of two distances.
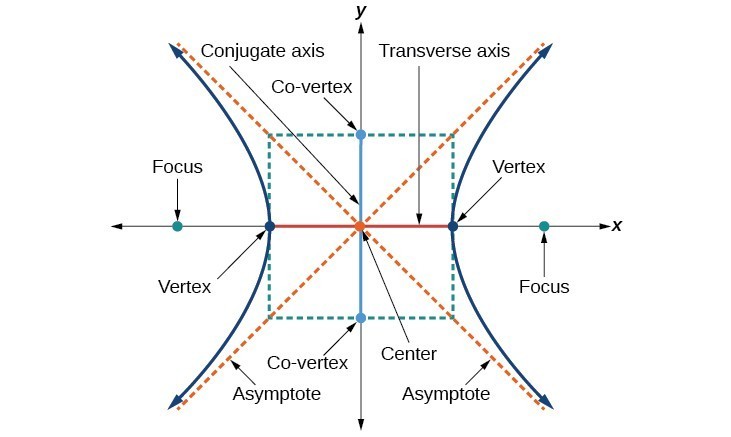
As with the ellipse, every hyperbola has two axes of symmetry. The transverse axis is a line segment that passes through the center of the hyperbola and has vertices as its endpoints. The foci lie on the line that contains the transverse axis. The conjugate axis is perpendicular to the transverse axis and has the co-vertices as its endpoints. The center of a hyperbola is the midpoint of both the transverse and conjugate axes, where they intersect. Every hyperbola also has two asymptotes that pass through its center. As a hyperbola recedes from the center, its branches approach these asymptotes. The central rectangle of the hyperbola is centered at the origin with sides that pass through each vertex and co-vertex; it is a useful tool for graphing the hyperbola and its asymptotes. To sketch the asymptotes of the hyperbola, simply sketch and extend the diagonals of the central rectangle.
You can view the transcript for “Conic Sections: The Hyperbola part 1 of 2” here (opens in new window).
You can view the transcript for “Conic Sections: The Hyperbola part 2 of 2” here (opens in new window).
Standard Form of the Equation of a Hyperbola Centered at the Origin
The Main Idea
- Horizontal Transverse Axis: [latex]\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1[/latex]
- Vertical Transverse Axis: [latex]\frac{y^2}{a^2} - \frac{x^2}{b^2} = 1[/latex]
- Key Features:
- Vertices: [latex](±a, 0)[/latex] or [latex](0, ±a)[/latex]
- Co-vertices: [latex](0, ±b)[/latex] or [latex](±b, 0)[/latex]
- Foci: [latex](±c, 0)[/latex] or [latex](0, ±c)[/latex], where [latex]c^2 = a^2 + b^2[/latex]
- Transverse axis length: [latex]2a[/latex]
- Conjugate axis length: [latex]2b[/latex]
- Asymptotes:
- Horizontal: [latex]y=\pm \dfrac{b}{a}x[/latex]
- Vertical: [latex]y=\pm \dfrac{a}{b}x[/latex]
Identifying Features from Equation
- Determine transverse axis orientation:
- [latex]x^2[/latex] positive: horizontal
- [latex]y^2[/latex] positive: vertical
- Find vertices:
- [latex]a = \sqrt{\text{term with positive coefficient}}[/latex]
- Find co-vertices:
- [latex]b = \sqrt{\text{term with negative coefficient}}[/latex]
- Calculate c:
- [latex]c = \sqrt{a^2 + b^2}[/latex]
- Asymptotes:
- Slope = [latex]\pm\frac{b}{a}[/latex] (horizontal) or [latex]\pm\frac{a}{b}[/latex] (vertical)
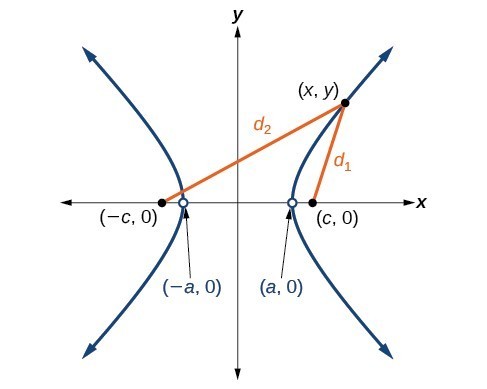
If [latex]\left(a,0\right)[/latex] is a vertex of the hyperbola, the distance from [latex]\left(-c,0\right)[/latex] to [latex]\left(a,0\right)[/latex] is [latex]a-\left(-c\right)=a+c[/latex]. The distance from [latex]\left(c,0\right)[/latex] to [latex]\left(a,0\right)[/latex] is [latex]c-a[/latex]. The difference of the distances from the foci to the vertex is
[latex]\left(a+c\right)-\left(c-a\right)=2a[/latex]
If [latex]\left(x,y\right)[/latex] is a point on the hyperbola, we can define the following variables:
[latex]\begin{align}&{d}_{2}=\text{the distance from }\left(-c,0\right)\text{ to }\left(x,y\right)\\ &{d}_{1}=\text{the distance from }\left(c,0\right)\text{ to }\left(x,y\right)\end{align}[/latex]
By definition of a hyperbola, [latex]\lvert{d}_{2}-{d}_{1}\rvert[/latex] is constant for any point [latex]\left(x,y\right)[/latex] on the hyperbola. We know that the difference of these distances is [latex]2a[/latex] for the vertex [latex]\left(a,0\right)[/latex]. It follows that [latex]\lvert{d}_{2}-{d}_{1}\rvert=2a[/latex] for any point on the hyperbola. The derivation of the equation of a hyperbola is based on applying the distance formula, but is again beyond the scope of this text. The standard form of an equation of a hyperbola centered at the origin with vertices [latex]\left(\pm a,0\right)[/latex] and co-vertices [latex]\left(0\pm b\right)[/latex] is [latex]\dfrac{{x}^{2}}{{a}^{2}}-\dfrac{{y}^{2}}{{b}^{2}}=1[/latex].
Writing Equations of Hyperbolas Centered at the Origin
The Main Idea
- Standard Forms:
- Horizontal: [latex]\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1[/latex]
- Vertical: [latex]\frac{y^2}{a^2} - \frac{x^2}{b^2} = 1[/latex]
- Relationship: [latex]c^2 = a^2 + b^2[/latex]
- Process:
- Identify transverse axis
- Determine [latex]a[/latex] from vertices
- Find [latex]c[/latex] from foci
- Calculate [latex]b[/latex] using [latex]c^2 = a^2 + b^2[/latex]
Steps to Write Equation
- Determine transverse axis orientation:
- [latex]x[/latex]-coordinates different: horizontal
- [latex]y[/latex]-coordinates different: vertical
- Identify [latex]a[/latex]:
- Distance from center to vertex
- Identify [latex]c[/latex]:
- Distance from center to focus
- Calculate [latex]b[/latex]:
- [latex]{b}^{2}={c}^{2}-{a}^{2}[/latex]
Hyperbolas Not Centered at the Origin
The Main Idea
- Standard Forms:
- Horizontal transverse axis: [latex]\frac{(x-h)^2}{a^2} - \frac{(y-k)^2}{b^2} = 1[/latex]
- Vertical transverse axis: [latex]\frac{(y-k)^2}{a^2} - \frac{(x-h)^2}{b^2} = 1[/latex]
- Key Features:
- Center: [latex](h, k)[/latex]
- Vertices: [latex](h ± a, k)[/latex] or [latex](h, k ± a)[/latex]
- Co-vertices: [latex](h, k ± b)[/latex] or [latex](h ± b, k)[/latex]
- Foci: [latex](h ± c, k)[/latex] or [latex](h, k ± c)[/latex], where [latex]c^2 = a^2 + b^2[/latex]
- Transverse Axis:
- Length: [latex]2a[/latex]
- Parallel to [latex]x[/latex]-axis if [latex]y[/latex]-coordinates of vertices and foci are the same
- Parallel to [latex]y[/latex]-axis if [latex]x[/latex]-coordinates of vertices and foci are the same
From Points to Equation
- Determine transverse axis orientation
- Find center using midpoint formula
- Calculate [latex]a[/latex] (half the distance between vertices)
- Find [latex]c[/latex] (distance from center to focus)
- Calculate [latex]b[/latex] using [latex]b^2 = c^2 - a^2[/latex]
- Substitute values into appropriate standard form
Graphing Hyperbolas
The Main Idea
- Standard Forms:
- Horizontal, origin: [latex]\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1[/latex]
- Vertical, origin: [latex]\frac{y^2}{a^2} - \frac{x^2}{b^2} = 1[/latex]
- Horizontal, center (h,k): [latex]\frac{(x-h)^2}{a^2} - \frac{(y-k)^2}{b^2} = 1[/latex]
- Vertical, center (h,k): [latex]\frac{(y-k)^2}{a^2} - \frac{(x-h)^2}{b^2} = 1[/latex]
- Key Features:
- Center: [latex](0,0)[/latex] or [latex](h,k)[/latex]
- Vertices: [latex](\pm a,0)[/latex], [latex](0,\pm a)[/latex], [latex](h\pm a,k)[/latex], or [latex](h,k\pm a)[/latex]
- Co-vertices: [latex](0,\pm b)[/latex], [latex](\pm b,0)[/latex], [latex](h,k\pm b)[/latex], or [latex](h\pm b,k)[/latex]
- Foci: [latex](\pm c,0)[/latex], [latex](0,\pm c)[/latex], [latex](h\pm c,k)[/latex], or [latex](h,k\pm c)[/latex], where [latex]c^2 = a^2 + b^2[/latex]
- Asymptotes:
- Centered at origin: [latex]y = \pm\frac{b}{a}x[/latex] or [latex]y = \pm\frac{a}{b}x[/latex]
- Centered at [latex](h,k)[/latex]: [latex]y = \pm\frac{b}{a}(x-h) + k[/latex] or [latex]y = \pm\frac{a}{b}(x-h) + k[/latex]
Graphing Process
- Identify the standard form and orientation
- Determine center, vertices, and co-vertices
- Calculate foci using [latex]c = \sqrt{a^2 + b^2}[/latex]
- Find asymptote equations
- Plot center, vertices, co-vertices, and foci
- Sketch asymptotes
- Draw hyperbola curves approaching asymptotes
For Non-Standard Form
- Group like terms
- Complete the square for [latex]x[/latex] and [latex]y[/latex]
- Rewrite as perfect squares
- Divide by constant to get standard form
- Follow steps for graphing standard form
You can view the transcript for “Ex 1: Conic Section – Graph a Hyperbola with Center at the Origin (Horizontal)” here (opens in new window).
You can view the transcript for “Ex 3: Conic Section – Graph a Hyperbola with Center NOT at the Origin (Horizontal)” here (opens in new window).