Identifying Zeros and Their Behavior
Before we start graphing polynomial functions, it’s essential to understand the key features that shape these graphs. One of the most important aspects is identifying the zeros of the polynomial. Zeros, or roots, are the points where the function crosses the x-axis.
But there’s more to zeros than just their locations. Graphs behave differently at various [latex]x[/latex]-intercepts. Sometimes, the graph will cross over the horizontal axis at an intercept. Other times, the graph will touch the horizontal axis and “bounce” off.
Suppose, for example, we graph the function [latex]f(x) = (x+3)(x-2)^2(x+1)^3[/latex]. Notice below that the behavior of the function at each of the [latex]x[/latex]-intercepts is different.
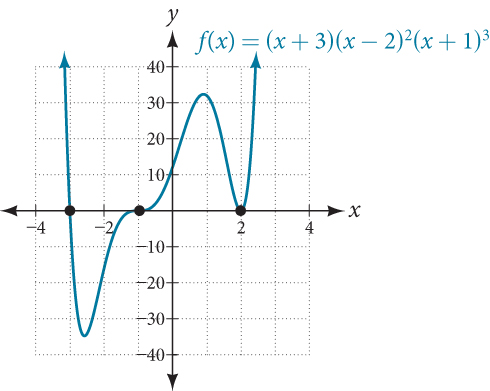
The [latex]x[/latex]-intercept [latex]x = -3[/latex] is the solution of the equation [latex](x + 3) = 0[/latex]. The graph passes directly through the [latex]x[/latex]-intercept at [latex]x = -3[/latex]. The factor is linear (has a degree of [latex]1[/latex]), so the behavior near the intercept is like that of a line—it passes directly through the intercept. We call this a single zero because the zero corresponds to a single factor of the function.
The [latex]x[/latex]-intercept [latex]x = 2[/latex] is the repeated solution of the equation [latex](x - 2)^2 = 0[/latex]. The graph touches the axis at the intercept and changes direction. The factor is quadratic (degree [latex]2[/latex]), so the behavior near the intercept is like that of a quadratic—it bounces off of the horizontal axis at the intercept.
[latex](x - 2)^2 = (x - 2)(x - 2)[/latex]
The factor is repeated, that is, the factor [latex](x - 2)[/latex] appears twice. The number of times a given factor appears in the factored form of the equation of a polynomial is called the multiplicity. The zero associated with this factor, [latex]x = 2[/latex], has multiplicity [latex]2[/latex] because the factor [latex](x - 2)[/latex] occurs twice.
The [latex]x[/latex]-intercept [latex]x = -1[/latex] is the repeated solution of factor [latex](x + 1)^3 = 0[/latex]. The graph passes through the axis at the intercept, but flattens out a bit first. This factor is cubic (degree [latex]3[/latex]), so the behavior near the intercept is like that of a cubic—with the same S-shape near the intercept as the toolkit function [latex]f(x) = x^3[/latex]. We call this a triple zero, or a zero with multiplicity [latex]3[/latex].
For zeros with even multiplicities, the graphs touch or are tangent to the [latex]x[/latex]-axis. For zeros with odd multiplicities, the graphs cross or intersect the [latex]x[/latex]-axis.
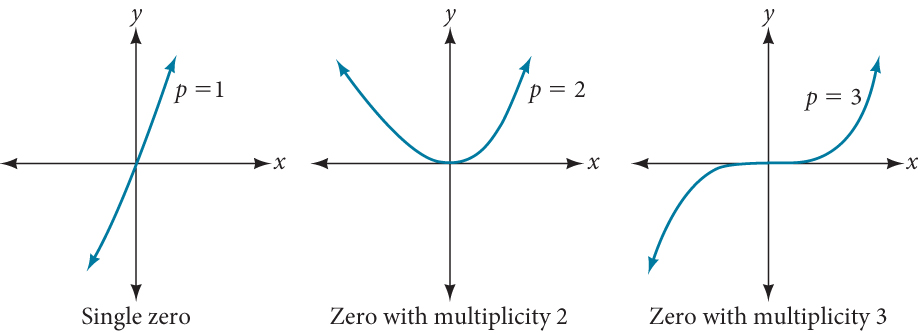
For higher even powers, such as [latex]4[/latex], [latex]6[/latex], and [latex]8[/latex], the graph will still touch and bounce off of the horizontal axis but, for each increasing even power, the graph will appear flatter as it approaches and leaves the [latex]x[/latex]-axis.
For higher odd powers, such as [latex]5[/latex], [latex]7[/latex], and [latex]9[/latex], the graph will still cross through the horizontal axis, but for each increasing odd power, the graph will appear flatter as it approaches and leaves the [latex]x[/latex]-axis.
graphical behavior of polynomials at [latex]x[/latex]-intercepts
If a polynomial contains a factor of the form [latex](x-h)^{p}[/latex], the behavior near the [latex]x[/latex]-intercept at [latex](h,0)[/latex] is determined by the power [latex]p[/latex]. We say that [latex]x=h[/latex] is a zero of multiplicity [latex]p[/latex].
- For zeros with even multiplicities, the graphs touch or are tangent to the [latex]x[/latex]-axis at these [latex]x[/latex]-values.
- For zeros with odd multiplicities, the graphs cross or intersect the [latex]x[/latex]-axis at these [latex]x[/latex]-values.
Note: The sum of the multiplicities is the degree of the polynomial function.
Given a graph of a polynomial function of degree [latex]n[/latex], identify the zeros and their multiplicities.
- If the graph crosses the [latex]x[/latex]-axis and appears almost linear at the intercept, it is a single zero.
- If the graph touches the [latex]x[/latex]-axis and bounces off of the axis, it is a zero with even multiplicity.
- If the graph crosses the [latex]x[/latex]-axis at a zero, it is a zero with odd multiplicity.
- The sum of the multiplicities is [latex]\leq n[/latex].

Use the graph of the function of degree [latex]6[/latex] to identify the zeros of the function and their possible multiplicities.