- Identify key features like zeros, turning points, and end behavior in graphs of polynomial functions
- Find where polynomial functions equal zero using different methods, and understand what these zeros mean
- Create and explain graphs of polynomial functions, connecting how the function is written to what its graph looks like
Recognizing Characteristics of Graphs of Polynomial Functions
Polynomial functions of degree 2 or more have graphs that do not have sharp corners; recall that these types of graphs are called smooth curves. Polynomial functions also display graphs that have no breaks. Curves with no breaks are called continuous. The figure below shows a graph that represents a polynomial function and a graph that represents a function that is not a polynomial.
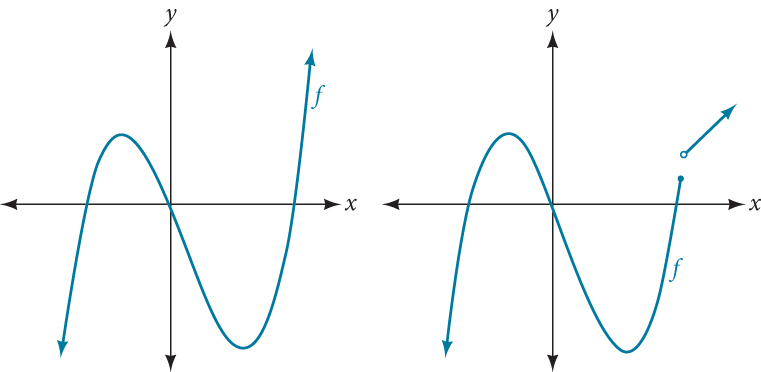
Do all polynomial functions have as their domain all real numbers?
Yes. Any real number is a valid input for a polynomial function.