Writing Equations of Parallel Lines
If we know the equation of a line, we can use what we know about slope to write the equation of a line that is either parallel or perpendicular to the given line.
[latex]f\left(x\right)=3x+1[/latex]
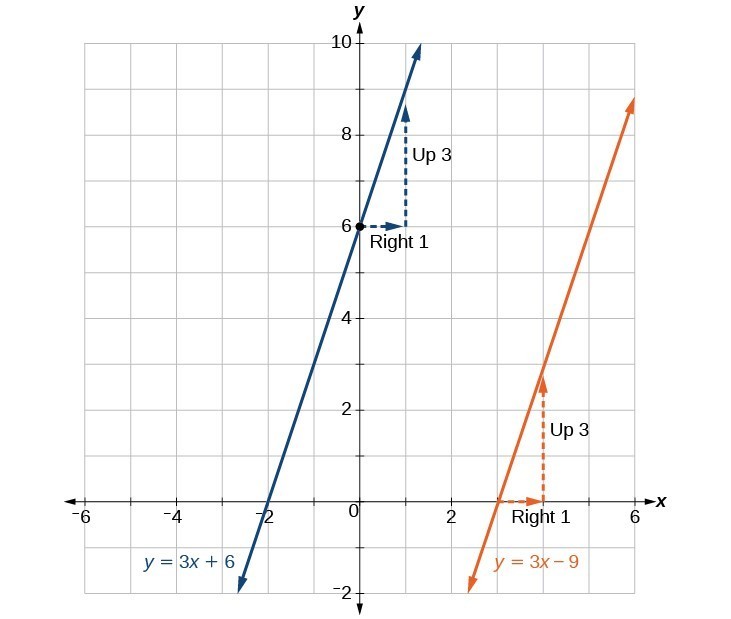
We know that the slope of the line is [latex]3[/latex]. We also know that the [latex]y[/latex]–intercept is [latex](0, 1)[/latex]. Any other line with a slope of [latex]3[/latex] will be parallel to [latex]f(x)[/latex]. The lines formed by all of the following functions will be parallel to [latex]f(x)[/latex].
[latex]\begin{array}{l}g\left(x\right)=3x+6\hfill \\ h\left(x\right)=3x+1\hfill \\ p\left(x\right)=3x+\frac{2}{3}\hfill \end{array}[/latex]
Suppose then we want to write the equation of a line that is parallel to [latex]f[/latex] and passes through the point [latex](1, 7)[/latex]. We already know that the slope is [latex]3[/latex]. We just need to determine which value for [latex]b[/latex] will give the correct line. We can begin by using point-slope form of an equation for a line. We can then rewrite it in slope-intercept form.
[latex]\begin{array}{l}y-{y}_{1}=m\left(x-{x}_{1}\right)\hfill \\ y - 7=3\left(x - 1\right)\hfill \\ y - 7=3x - 3\hfill \\ \text{}y=3x+4\hfill \end{array}[/latex]
So [latex]g\left(x\right)=3x+4[/latex] is parallel to [latex]f\left(x\right)=3x+1[/latex] and passes through the point [latex](1, 7)[/latex].
- Find the slope of the function.
- Substitute the slope and given point into point-slope or slope-intercept form.
- Simplify.
Writing Equations of Perpendicular Lines
We can use a very similar process to write the equation of a line perpendicular to a given line. Instead of using the same slope, however, we use the negative reciprocal of the given slope.
[latex]f\left(x\right)=2x+4[/latex]
The slope of the line is [latex]2[/latex], and its negative reciprocal is [latex]-\frac{1}{2}[/latex]. Any function with a slope of [latex]-\frac{1}{2}[/latex] will be perpendicular to [latex]f(x)[/latex]. The lines formed by all of the following functions will be perpendicular to [latex]f(x)[/latex].
[latex]\begin{array}{l}g\left(x\right)=-\frac{1}{2}x+4\hfill \\ h\left(x\right)=-\frac{1}{2}x+2\hfill \\ p\left(x\right)=-\frac{1}{2}x-\frac{1}{2}\hfill \end{array}[/latex]
As before, we can narrow down our choices for a particular perpendicular line if we know that it passes through a given point. Suppose that we want to write the equation of a line that is perpendicular to [latex]f(x)[/latex] and passes through the point [latex](4, 0)[/latex]. We already know that the slope is [latex]-\frac{1}{2}[/latex]. Now we can use the point to find the [latex]y[/latex]-intercept by substituting the given values into the slope-intercept form of a line and solving for [latex]b[/latex].
[latex]\begin{array}{l}g\left(x\right)=mx+b\hfill \\ 0=-\frac{1}{2}\left(4\right)+b\hfill \\ 0=-2+b\hfill \\ 2=b\hfill \\ b=2\hfill \end{array}[/latex]
The equation for the function with a slope of [latex]-\frac{1}{2}[/latex] and a [latex]y[/latex]–intercept of [latex]2[/latex] is
[latex]g\left(x\right)=-\frac{1}{2}x+2[/latex].
So [latex]g\left(x\right)=-\frac{1}{2}x+2[/latex] is perpendicular to [latex]f\left(x\right)=2x+4[/latex] and passes through the point [latex](4, 0)[/latex].
- Find the slope of the given function.
- Determine the negative reciprocal of the slope.
- Substitute the new slope and the values for [latex]x[/latex] and [latex]y[/latex] from given point into [latex]g\left(x\right)=mx+b[/latex].
- Solve for [latex]b[/latex].
- Write the equation of the line.
- Determine the slope of the line passing through the points.
- Find the negative reciprocal of the slope.
- Use slope-intercept form or point-slope form to write the equation by substituting the known values.
- Simplify.