Determining Whether Lines are Parallel or Perpendicular
The two lines in the graph below are parallel lines: they will never intersect. Notice that they have exactly the same steepness which means their slopes are identical. The only difference between the two lines is the y-intercept. If we shifted one line vertically toward the y-intercept of the other, they would become the same line.
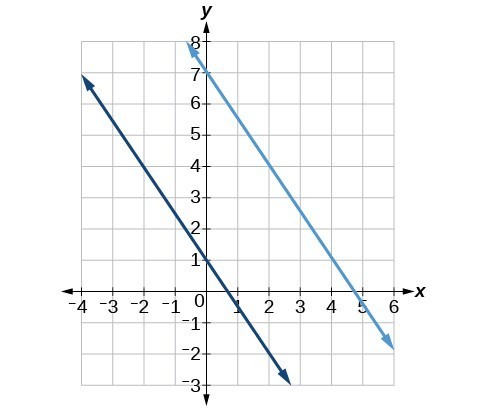
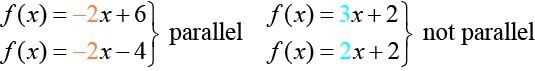
We can determine from their equations whether two lines are parallel by comparing their slopes. If the slopes are the same and the [latex]y[/latex]-intercepts are different, the lines are parallel. If the slopes are different, the lines are not parallel.
Unlike parallel lines, perpendicular lines do intersect. Their intersection forms a right or[latex]90[/latex]-degree angle. The two lines below are perpendicular.
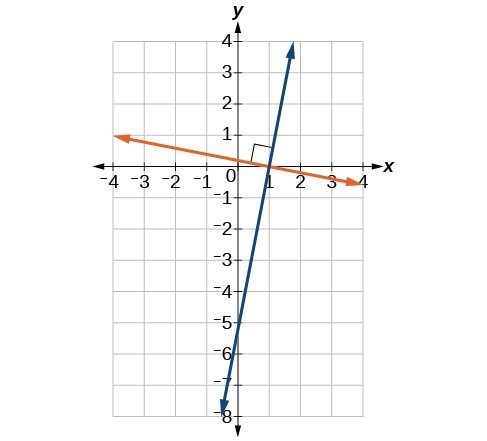
Perpendicular lines do not have the same slope. The slopes of perpendicular lines are different from one another in a specific way. The slope of one line is the negative reciprocal of the slope of the other line.
[latex]{m}_{1}*{m}_{2}=-1[/latex]
To find the reciprocal of a number, divide [latex]1[/latex] by the number. So the reciprocal of [latex]8[/latex] is [latex]\frac{1}{8}[/latex], and the reciprocal of [latex]\frac{1}{8}[/latex] is [latex]8[/latex]. To find the negative reciprocal, first find the reciprocal and then change the sign.
As with parallel lines, we can determine whether two lines are perpendicular by comparing their slopes. The slope of each line below is the negative reciprocal of the other so the lines are perpendicular.
[latex]\begin{array}{ll}f\left(x\right)=\frac{1}{4}x+2\hfill & \text{negative reciprocal of }\frac{1}{4}\text{ is }-4\hfill \\ f\left(x\right)=-4x+3\hfill & \text{negative reciprocal of }-4\text{ is }\frac{1}{4}\hfill \end{array}[/latex]
The product of the slopes is [latex]–1[/latex].
[latex]-4\left(\frac{1}{4}\right)=-1[/latex]
parallel and perpendicular lines
Two lines are parallel lines if they do not intersect. The slopes of the lines are the same.
If and only if [latex]{b}_{1}={b}_{2}[/latex] and [latex]{m}_{1}={m}_{2}[/latex], we say the lines coincide. Coincident lines are the same line.
[latex]\\[/latex]
Two lines are perpendicular lines if they intersect at right angles.
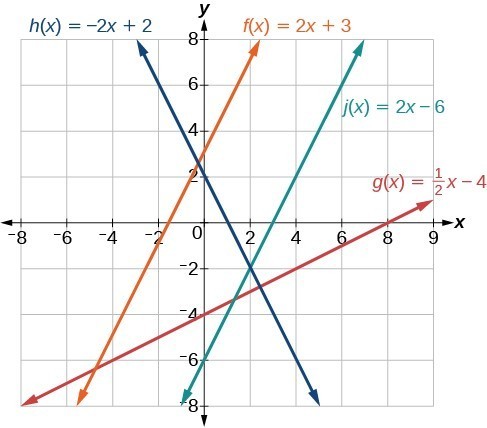
[latex]\begin{array}{l}f\left(x\right)=2x+3\hfill & \hfill & h\left(x\right)=-2x+2\hfill \\ g\left(x\right)=\frac{1}{2}x - 4\hfill & \hfill & j\left(x\right)=2x - 6\hfill \end{array}[/latex]