- Create and interpret equations of linear functions
- Identify and graph lines that are vertical or horizontal
- Graph straight lines by plotting points, using slope and y-intercept, and make changes like shifts to graphs
- Write equations for lines that run parallel or at a right angle to another line
Writing and Interpreting an Equation for a Linear Function
The Main Idea
- Forms of Linear Equations
- Slope-intercept form: [latex]y = mx + b[/latex]
- Point-slope form: [latex]y - y_1 = m(x - x_1)[/latex]
- Essential Components
- Slope (m): Rate of change
- y-intercept (b): Point where the line crosses the y-axis
- Determining the Equation
- From a graph
- From two points
- From a point and slope
Graphical Approach
- Identify two points on the line
- Calculate the slope: [latex]m = \frac{y_2 - y_1}{x_2 - x_1}[/latex]
- Find the y-intercept visually or by calculation
- Formulate the equation: [latex]y = mx + b[/latex]
Algebraic Approach
- Given two points: [latex](x_1, y_1)[/latex] and [latex](x_2, y_2)[/latex]
- Calculate slope: [latex]m = \frac{y_2 - y_1}{x_2 - x_1}[/latex]
- Use point-slope form: [latex]y - y_1 = m(x - x_1)[/latex]
- Rearrange to slope-intercept form if needed
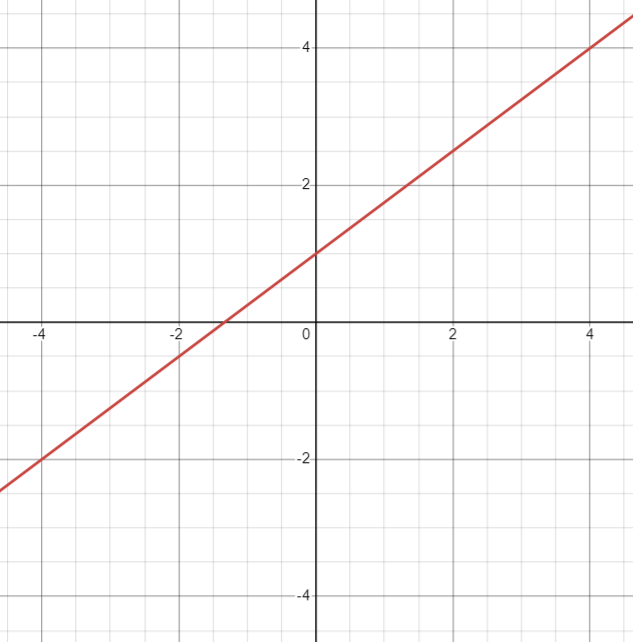
Consider the following graph of a linear function given below. Find the equation of this line in slope-intercept form.
Describing Horizontal and Vertical Lines
The Main Idea
- Horizontal Lines
- Equation: [latex]y = b[/latex] or [latex]f(x) = b[/latex], where [latex]b[/latex] is constant
- Slope: [latex]m = 0[/latex]
- [latex]Y[/latex]-intercept = [latex](0, b)[/latex]
- No [latex]x[/latex]-intercept (unless [latex]b = 0[/latex])
- Represent constant output ([latex]y[/latex]-value)
- Parallel to [latex]x[/latex]-axis
- Vertical Lines
- Equation: [latex]x = a[/latex], where [latex]a[/latex] is constant
- Slope: Undefined
- No [latex]y[/latex]-intercept (unless [latex]a = 0[/latex])
- [latex]X[/latex]-intercept = [latex](a, 0)[/latex]
- Represent constant input ([latex]x[/latex]-value)
- Not a function
- Parallel to [latex]y[/latex]-axis
Graphing Linear Functions
The Main Idea
- Three primary methods for graphing linear functions:
- Plotting points
- Using y-intercept and slope
- Applying transformations to [latex]f(x) = x[/latex]
- Linear function equation: [latex]f(x) = mx + b[/latex]
- [latex]m[/latex]: slope (rate of change)
- [latex]b[/latex]: [latex]y[/latex]-intercept (where the line crosses the [latex]y[/latex]-axis)
- Slope-intercept form provides direct access to key graph characteristics
- Transformations of the identity function offer insights into function behavior
- Each method provides unique perspectives on the function’s properties
Method 1: Plotting Points
Steps:
- Choose at least two input values ([latex]x[/latex]-coordinates)
- Calculate corresponding output values ([latex]y[/latex]-coordinates)
- Plot the points on a coordinate plane
- Draw a line through the points
Method 2: Using [latex]y[/latex]-intercept and Slope
Key Concepts:
- y-intercept ([latex]b[/latex]): Point where the line crosses the y-axis [latex](0, b)[/latex]
- Slope ([latex]m[/latex]): Rate of change, [latex]m = \frac{\text{rise}}{\text{run}} = \frac{\Delta y}{\Delta x}[/latex]
Steps:
- Identify the y-intercept ([latex]b[/latex])
- Identify the slope ([latex]m[/latex])
- Plot the [latex]y[/latex]-intercept
- Use the slope to plot additional points
- Draw the line through the points
Method 3: Transformations of [latex]f(x) = x[/latex]
Key Transformations:
- Vertical stretch/compression: [latex]f(x) = mx[/latex]
- Vertical shift: [latex]f(x) = x + b[/latex]
Steps:
- Start with [latex]f(x) = x[/latex]
- Apply vertical stretch/compression by factor [latex]m[/latex]
- Apply vertical shift by [latex]b[/latex] units
You can view the transcript for “Graph a Linear Function as a Transformation of f(x)=x” here (opens in new window).
Determining Whether Lines are Parallel or Perpendicular
The Main Idea
- Parallel lines never intersect and have the same slope.
-
Key characteristics:
- Same slope ([latex]m[/latex])
- Different y-intercept ([latex]b[/latex])
- Equation form: [latex]y = mx + b_1[/latex] and [latex]y = mx + b_2[/latex], where [latex]b_1 \neq b_2[/latex]
-
- Perpendicular lines intersect at a 90-degree angle and have slopes that are negative reciprocals of each other.
-
Key characteristics:
- Slopes are negative reciprocals: [latex]m_1 = -\frac{1}{m_2}[/latex]
- Product of slopes equals [latex]-1[/latex]: [latex]m_1 \cdot m_2 = -1[/latex]
- Equation form: [latex]y = m_1x + b_1[/latex] and [latex]y = -\frac{1}{m_1}x + b_2[/latex]
-
- The slope-intercept form of a line ([latex]y = mx + b[/latex]) is key to identifying parallel and perpendicular lines.
You can view the transcript for “How To Tell If Two Lines Are Parallel, Perpendicular, or Neither?” here (opens in new window).
Writing Equations of Parallel and Perpendicular Lines
The Main Idea
- Parallel lines have the same slope but different [latex]y[/latex]-intercepts.
- Perpendicular lines have slopes that are negative reciprocals of each other.
- Point-slope form and slope-intercept form are key tools for writing these equations.
- Given a line and a point, we can write equations of parallel or perpendicular lines passing through that point.
- The process involves manipulating slopes and using known points to determine y-intercepts.
Writing Equations of Parallel Lines
Given a line [latex]f(x) = mx + b[/latex] and a point [latex](x_0, y_0)[/latex], to write the equation of a parallel line through the point:
- Identify the slope [latex]m[/latex] of the original line.
- Use point-slope form with the new point: [latex]y - y_0 = m(x - x_0)[/latex]
- Simplify to slope-intercept form: [latex]y = mx + (y_0 - mx_0)[/latex]
Writing Equations of Perpendicular Lines
Given a line [latex]f(x) = mx + b[/latex] and a point [latex](x_0, y_0)[/latex], to write the equation of a perpendicular line through the point:
- Find the negative reciprocal of the slope: [latex]m_{\perp} = -\frac{1}{m}[/latex]
- Use point-slope form with the new point: [latex]y - y_0 = m_{\perp}(x - x_0)[/latex]
- Simplify to slope-intercept form: [latex]y = m_{\perp}x + (y_0 - m_{\perp}x_0)[/latex]
Given [latex]f(x) = 3x + 1[/latex] and point [latex](2, 7)[/latex], find a parallel line.
Given [latex]f(x) = 2x + 4[/latex] and point [latex](3, 1)[/latex], find a perpendicular line.


