Slope of a Linear Equation
The slope of a line refers to the ratio of the vertical change in y over the horizontal change in x between any two points on a line. It indicates the direction in which a line slants as well as its steepness. Slope is sometimes described as rise over run.
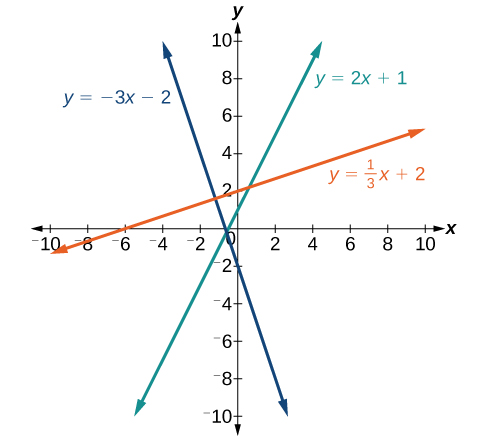
If the slope is positive, the line slants upward to the right. If the slope is negative, the line slants downward to the right. As the slope increases, the line becomes steeper. Some examples are shown below. The lines indicate the following slopes: [latex]m=-3[/latex], [latex]m=2[/latex], and [latex]m=\frac{1}{3}[/latex].
Slope of a Line
The slope of a line is a measure of its steepness or the angle at which it tilts, expressed as the ratio of the rise (the vertical change) to the run (the horizontal change) between any two points on the line. It quantifies how much the line goes up or down as it moves from left to right.
- A positive slope means that the line rises from left to right.
- A negative slope means that the line falls from left to right.
- A slope of zero means the line is flat.
Mathematically, the slope is calculated by its rise-to-run ratio:
[latex]\text{slope} = \dfrac{\text{rise}}{\text{run}}[/latex]

Given two points, [latex]\left({x}_{1},{y}_{1}\right)[/latex] and [latex]\left({x}_{2},{y}_{2}\right)[/latex], the following formula determines the slope of a line containing these points:
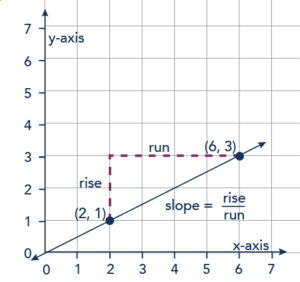
- Choose points that are clear and easy to identify on the graph. This often means selecting points where the line crosses grid lines, as the coordinates are straightforward to read.
- Start by selecting the clearest leftmost point where the line intersects the grid, then choose a second point to the right, ensuring it also clearly falls on a grid intersection.
- Measure the vertical change (rise), noting if it increases (positive) or decreases (negative), then measure the horizontal distance (run), which is always positive as you move from left to right, to calculate the slope.