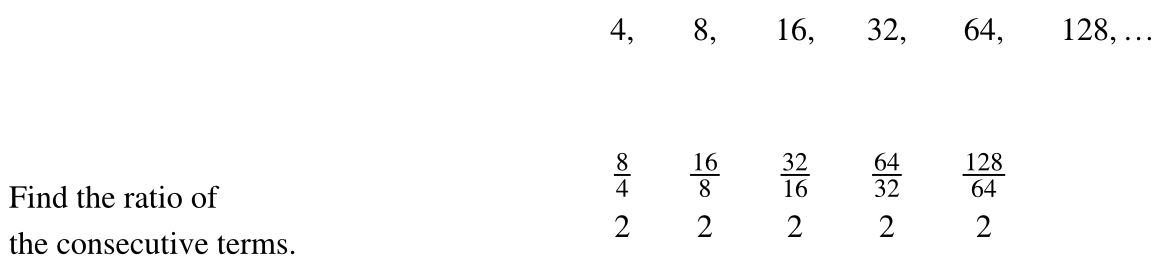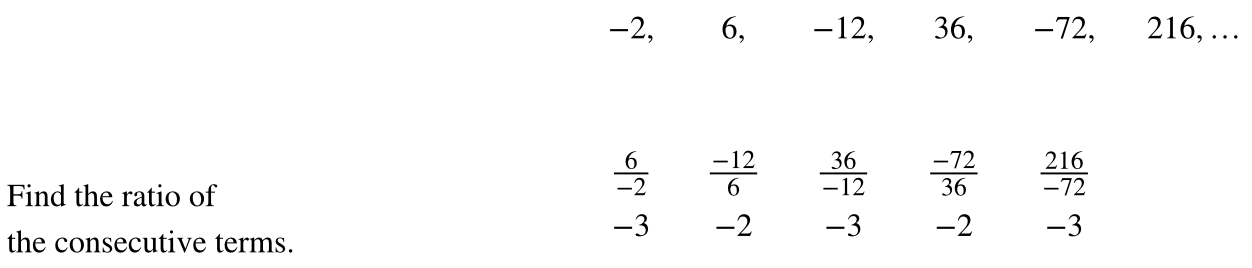Geometric Sequences: Learn It 1

  • Determine if a sequence is geometric, find the common ratio, list the terms, and find the general (nth) term of a geometric sequence
  • Use recursive and explicit formulas to describe and study geometric sequences

Geometric Sequence

Many companies offer an annual cost-of-living increase to keep salaries consistent with inflation. Let’s consider, for example, a recent college graduate who lands a position as a junior software developer with a starting annual salary of $[latex]54,000[/latex]. The company promises a [latex]2 \%[/latex] cost of living increase each year.

To calculate the developer’s salary in any given year, we multiply their salary from the previous year by [latex]102 \%[/latex]. Let’s see how this plays out over the first few years:

  • After one year: [latex]$54,000 \times 1.02 = $55,080[/latex]
  • After two years: [latex]$55,080 \times 1.02 = $56,181.60[/latex]
  • After three years: [latex]$56,181.60 \times 1.02 = $57,305.23[/latex]

As we can see, when a salary increases by a constant rate each year, it grows by a constant factor. In this case, the factor is [latex]1.02[/latex] or [latex]102 \%[/latex] of the previous year’s salary.

The yearly salary values described form a geometric sequence because they change by a constant factor each year. Each term of a geometric sequence increases or decreases by a constant factor called the common ratio.

geometric sequence

A sequence is called a geometric sequence if the ratio between consecutive terms is always the same.
The ratio between consecutive terms in a geometric sequence is [latex]r[/latex], the common ratio, where [latex]n \ge 2[/latex].

[latex]r = \dfrac{a_n}{a_{n-1}}[/latex]

 

The geometric sequence will be

[latex]\left\{{a}_{1}, {a}_{1}r,{a}_{1}{r}^{2},{a}_{1}{r}^{3},...\right\}[/latex]

The sequence below is an example of a geometric sequence because each term increases by a constant factor of [latex]6[/latex]. Multiplying any term of the sequence by the common ratio [latex]r = 6[/latex] generates the subsequent term.A sequence , {1, 6, 36, 216, 1296, ...} that shows all the numbers have a common ratio of 6.
How To: Given a set of numbers, determine if they represent a geometric sequence.

  1. Divide each term by the previous term.
  2. Compare the quotients. If they are the same, a common ratio exists and the sequence is geometric.
Determine if the follow sequences are geometric? If so, find the common ratio.

  • [latex]4, 8, 16, 32, 64, 128, \dots[/latex]

  • [latex]-2, 6, -12, 36, -72, 216, \dots[/latex]