Fitting Linear Models to Data: Learn It 3

Drawing and Interpreting Scatterplots

A professor is attempting to identify trends among final exam scores. His class has a mixture of students, so he wonders if there is any relationship between age and final exam scores. One way for him to analyze the scores is by creating a diagram that relates the age of each student to the exam score received. In this section, we will examine one such diagram known as a scatter plot.

When expressing pairs of inputs and outputs on a graph, they take the form of (input, output). In scatter plots, the two variables relate to create each data point, (variable 1, variable 2), but it is often not necessary to declare that one is dependent on the other. In the example below, each Age coordinate corresponds to a Final Exam Score in the form (age, score). Each corresponding pair is plotted on the graph.

A scatter plot is a graph of plotted points that may show a relationship between two sets of data. If the relationship is from a linear model, or a model that is nearly linear, the professor can draw conclusions using his knowledge of linear functions. Below is a sample scatter plot.

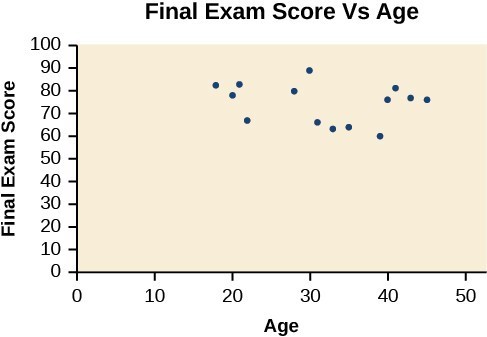
Scatter plot, titled 'Final Exam Score VS Age'. The x-axis is the age, and the y-axis is the final exam score. The range of ages are between 20s - 50s, and the range for scores are between upper 50s and 90s.
A scatter plot of age and final exam score variables.

Notice this scatter plot does not indicate a linear relationship. The points do not appear to follow a trend. In other words, there does not appear to be a relationship between the age of the student and the score on the final exam.

The table below shows the number of cricket chirps in [latex]15[/latex] seconds, for several different air temperatures, in degrees Fahrenheit.[1]

Chirps [latex]44[/latex] [latex]35[/latex] [latex]20.4[/latex] [latex]33[/latex] [latex]31[/latex] [latex]35[/latex] [latex]18.5[/latex] [latex]37[/latex] [latex]26[/latex]
Temperature [latex]80.5[/latex] [latex]70.5[/latex] [latex]57[/latex] [latex]66[/latex] [latex]68[/latex] [latex]72[/latex] [latex]52[/latex] [latex]73.5[/latex] [latex]53[/latex]

Let’s plot the data to determine whether the data appears to have a linear relationship.

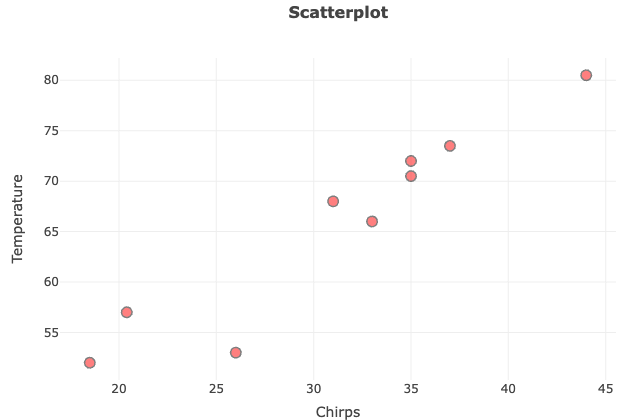
What do you think? Does it have a linear relationship?

  1. Selected data from http://classic.globe.gov/fsl/scientistsblog/2007/10/. Retrieved Aug 3, 2010 ↵