Exponential Functions

For the following exercises, identify whether the statement represents an exponential function. Explain.

1. A population of bacteria decreases by a factor of [latex]\dfrac{1}{8}[/latex] every [latex]24[/latex] hours.
2. For each training session, a personal trainer charges his clients [latex]$5[/latex] less than the previous training session.

For the following exercises, consider this scenario: For each year [latex]t[/latex], the population of a forest of trees is represented by the function [latex]A(t) = 115(1.025)^t[/latex]. In a neighboring forest, the population of the same type of tree is represented by the function [latex]B(t) = 82(1.029)^t[/latex]. (Round answers to the nearest whole number.)

3. Which forest’s population is growing at a faster rate?
4. Assuming the population growth models continue to represent the growth of the forests, which forest will have a greater number of trees after [latex]20[/latex] years? By how many?

For the following exercises, determine whether the equation represents exponential growth, exponential decay, or neither. Explain.

5. [latex]y = 220(1.06)^x[/latex]
6. [latex]y = 11,701(0.97)^t[/latex]

For the following exercises, find the formula for an exponential function that passes through the two points given.

7. [latex](0, 2000)[/latex] and [latex](2, 20)[/latex]
8. [latex]\left(-1, \dfrac{3}{2}\right)[/latex] and [latex](3, 24)[/latex]

For the following exercises, determine whether the table could represent a function that is linear, exponential, or neither. If it appears to be exponential, find a function that passes through the points.

9. [latex]x[/latex]	[latex]1[/latex]	[latex]2[/latex]	[latex]3[/latex]	[latex]4[/latex]
   [latex]f(x)[/latex]	[latex]70[/latex]	[latex]40[/latex]	[latex]10[/latex]	[latex]-20[/latex]

10. [latex]x[/latex]	[latex]1[/latex]	[latex]2[/latex]	[latex]3[/latex]	[latex]4[/latex]
    [latex]m(x)[/latex]	[latex]80[/latex]	[latex]61[/latex]	[latex]42.9[/latex]	[latex]25.61[/latex]

11. [latex]x[/latex]	[latex]1[/latex]	[latex]2[/latex]	[latex]3[/latex]	[latex]4[/latex]
    [latex]g(x)[/latex]	[latex]-3.25[/latex]	[latex]2[/latex]	[latex]7.25[/latex]	[latex]12.5[/latex]

For the following exercises, evaluate each function. Round answers to four decimal places, if necessary.

12. [latex]f(x) = -4^{2x+3}[/latex], for [latex]f(-1)[/latex]
13. [latex]f(x) = -2e^{x-1}[/latex], for [latex]f(-1)[/latex]
14. [latex]f(x) = 1.2e^{2x} - 0.3[/latex], for [latex]f(3)[/latex]

For the following exercises, determine the equation of the new function, [latex]g(x)[/latex]. State its [latex]y[/latex]-intercept, domain, and range.

15. [latex]f(x) = 3^x[/latex] is reflected about the [latex]y[/latex]-axis and stretched vertically by a factor of [latex]4[/latex]. What is the equation of the new function, [latex]g(x)[/latex]?
16. [latex]f(x) = 10^x[/latex] is reflected about the [latex]x[/latex]-axis and shifted upward [latex]7[/latex] units. What is the equation of the new function, [latex]g(x)[/latex]?
17. [latex]f(x) = -\dfrac{1}{2}\left(\dfrac{1}{4}\right)^{x-2} + 4[/latex] is shifted downward [latex]4[/latex] units, then shifted left [latex]2[/latex] units, stretched vertically by a factor of [latex]4[/latex], and reflected about the [latex]x[/latex]-axis. What is the equation of the new function, [latex]g(x)[/latex]?

For the following exercise, graph the function and its reflection about the [latex]y[/latex]-axis on the same axes, and give the [latex]y[/latex]-intercept.

18. [latex]g(x) = -2(0.25)^x[/latex]

For the following exercise, graph each set of functions on the same axes.

19. [latex]f(x) = 3\left(\dfrac{1}{4}\right)^x[/latex], [latex]g(x) = 3(2)^x[/latex], and [latex]h(x) = 3(4)^x[/latex]

For the following exercises, match each function with one of the graphs in the figure below.

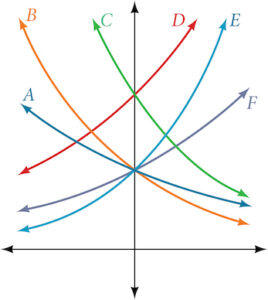
20. [latex]f(x) = 2(0.69)^x[/latex]
21. [latex]f(x) = 2(0.81)^x[/latex]
22. [latex]f(x) = 2(1.59)^x[/latex]

For the following exercises, use the graphs shown in the figure below. All have the form [latex]f(x) = ab^x[/latex].

23. Which graph has the largest value for [latex]b[/latex]?
24. Which graph has the largest value for [latex]a[/latex]?

For the following exercises, start with the graph of [latex]f(x) = 4^x[/latex]. Then write a function that results from the given transformation.

25. Shift [latex]f(x)[/latex] 3 units downward
26. Shift [latex]f(x)[/latex] 5 units right
27. Reflect [latex]f(x)[/latex] about the [latex]y[/latex]-axis

For the following exercise, each graph is a transformation of [latex]y=2^x[/latex]. Write an equation describing the transformation.

28. 

For the following exercise, find an exponential equation for the graph.

29. 

Applications of Exponential Functions

For the following exercises, use the compound interest formula, [latex]A(t) = P\left(1 + \dfrac{r}{n}\right)^{nt}[/latex]. After a certain number of years, the value of an investment account is represented by the equation [latex]A = 10,250(1 + \dfrac{0.04}{12})^{120}[/latex].

1. What was the initial deposit made to the account?
2. An account is opened with an initial deposit of [latex]$6,500[/latex] and earns [latex]3.6\%[/latex] interest compounded semi-annually. What will the account be worth in [latex]20[/latex] years?
3. Solve the compound interest formula for the principal, [latex]P[/latex].
4. How much more would the account in the previous two exercises be worth if it were earning interest for [latex]5[/latex] more years?
5. Use the formula found in the previous exercise to calculate the interest rate for an account that was compounded semi-annually, had an initial deposit of [latex]$9,000[/latex] and was worth [latex]$13,373.53[/latex] after [latex]10[/latex] years.

For the following exercises, determine whether the equation represents continuous growth, continuous decay, or neither. Explain.

6. [latex]y = 3742(e)^{0.75t}[/latex]
7. [latex]y = 2.25(e)^{-2t}[/latex]

8. The fox population in a certain region has an annual growth rate of [latex]9\%[/latex] per year. In the year [latex]2012[/latex], there were [latex]23,900[/latex] fox counted in the area. What is the fox population predicted to be in the year [latex]2020[/latex]?
9. In the year [latex]1985[/latex], a house was valued at [latex]$110,000[/latex]. By the year [latex]2005[/latex], the value had appreciated to [latex]$145,000[/latex]. What was the annual growth rate between [latex]1985[/latex] and [latex]2005[/latex]? Assume that the value continued to grow by the same percentage. What was the value of the house in the year [latex]2010[/latex]?
10. Jaylen wants to save [latex]$54,000[/latex] for a down payment on a home. How much will he need to invest in an account with [latex]8.2\%[/latex] APR, compounding daily, in order to reach his goal in [latex]5[/latex] years?
11. Alyssa opened a retirement account with [latex]7.25\%[/latex] APR in the year [latex]2000[/latex]. Her initial deposit was [latex]$13,500[/latex]. How much will the account be worth in [latex]2025[/latex] if interest compounds monthly? How much more would she make if interest compounded continuously?

Logarithmic Functions

For the following exercises, rewrite each equation in exponential form.

1. [latex]\log_a(b) = c[/latex]
2. [latex]\log_x(64) = y[/latex]
3. [latex]\log_{15}(a) = b[/latex]

For the following exercises, rewrite each equation in logarithmic form.

4. [latex]c^d = k[/latex]
5. [latex]19^x = y[/latex]
6. [latex]y^x = \dfrac{39}{100}[/latex]

For the following exercises, solve for [latex]x[/latex] by converting the logarithmic equation to exponential form.

7. [latex]\log_2(x) = -3[/latex]
8. [latex]\log_3(x) = 3[/latex]
9. [latex]\log_9(x) = \dfrac{1}{2}[/latex]

For the following exercises, use the definition of common and natural logarithms to simplify.

10. [latex]10^{\log(32)}[/latex]
11. [latex]e^{\ln(1.06)}[/latex]
12. [latex]e^{\ln(10.125)} + 4[/latex]

For the following exercises, evaluate the base [latex]b[/latex] logarithmic expression without using a calculator.

13. [latex]\log_6(\sqrt{6})[/latex]
14. [latex]6\log_8(4)[/latex]

For the following exercises, evaluate the common logarithmic expression without using a calculator.

15. [latex]\log(0.001)[/latex]
16. [latex]2\log(100^{-3})[/latex]

For the following exercises, evaluate the natural logarithmic expression without using a calculator.

17. [latex]\ln(1)[/latex]
18. [latex]25\ln\left(e^{\frac{2}{5}}\right)[/latex]

Logarithmic Function Graphs and Characteristics

For the following exercises, state the domain and range of the function.

1. [latex]h(x) = \ln\left(\dfrac{1}{2} - x\right)[/latex]
2. [latex]h(x) = \ln(4x + 17) - 5[/latex]

For the following exercises, state the domain and the vertical asymptote of the function.

3. [latex]f(x) = \log_b(x - 5)[/latex]
4. [latex]f(x) = \log(3x + 1)[/latex]
5. [latex]g(x) = -\ln(3x + 9) - 7[/latex]

For the following exercises, state the domain, range, and [latex]x[/latex]– and [latex]y[/latex]-intercepts, if they exist. If they do not exist, write [latex]DNE[/latex].

6. [latex]h(x) = \log_4(x - 1) + 1[/latex]
7. [latex]g(x) = \ln(-x) - 2[/latex]
8. [latex]h(x) = 3\ln(x) - 9[/latex]

For the following exercises, match each function in the figure below with the letter corresponding to its graph.

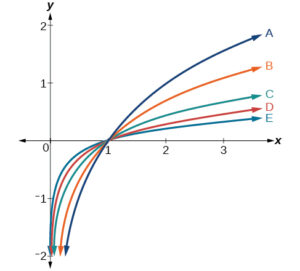
9. [latex]f(x) = \ln(x)[/latex]
10. [latex]h(x) = \log_5(x)[/latex]

For the following exercises, match each function in the figure below with the letter corresponding to its graph.

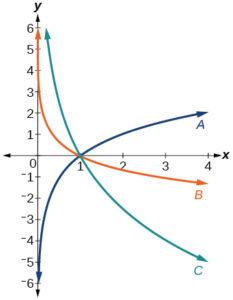
11. [latex]f(x) = \log_{\frac{1}{3}}(x)[/latex]
12. [latex]h(x) = \log_{\frac{3}{4}}(x)[/latex]

For the following exercises, sketch the graphs of each pair of functions on the same axis.

13. [latex]f(x) = \log(x)[/latex] and [latex]g(x) = \log_{\frac{1}{2}}(x)[/latex]
14. [latex]f(x) = e^x[/latex] and [latex]g(x) = \ln(x)[/latex]

For the following exercises, sketch the graph of the indicated function.

15. [latex]f(x) = \log_2(x + 2)[/latex]
16. [latex]f(x) = \ln(-x)[/latex]
17. [latex]g(x) = \log(6 - 3x) + 1[/latex]

For the following exercises, write a logarithmic equation corresponding to the graph shown.

18. Use [latex]y = \log_2(x)[/latex] as the parent function.
    
19. Use [latex]f(x) = \log_4(x)[/latex] as the parent function.