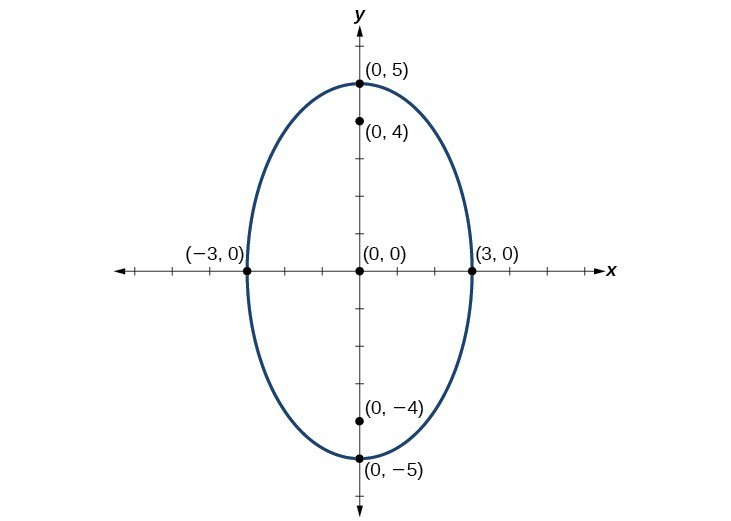
Writing Equations and Graphing Ellipses Centered at the Origin in Standard Form
The key features of the ellipse are its center, vertices, co-vertices, foci, and lengths and positions of the major and minor axes. Just as with other equations, we can identify all of these features just by looking at the standard form of the equation. There are four variations of the standard form of the ellipse. These variations are categorized first by the location of the center (the origin or not the origin), and then by the position (horizontal or vertical). Each is presented along with a description of how the parts of the equation relate to the graph. Interpreting these parts allows us to form a mental picture of the ellipse.
standard forms of the equation of an ellipse with center [latex](0,0)[/latex]
The standard form of the equation of an ellipse with center [latex]\left(0,0\right)[/latex] and major axis parallel to the [latex]x[/latex]-axis is
[latex]\dfrac{{x}^{2}}{{a}^{2}}+\dfrac{{y}^{2}}{{b}^{2}}=1[/latex]
where:
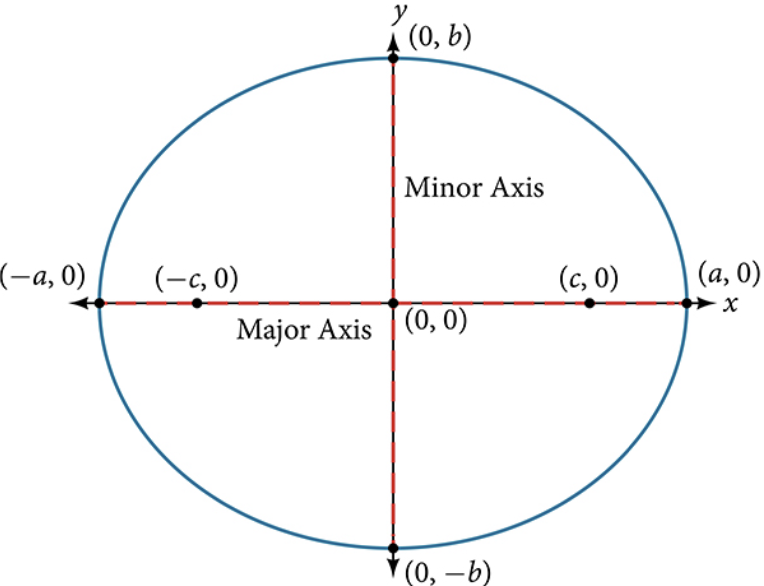
- [latex]a>b[/latex]
- the length of the major axis is [latex]2a[/latex]
- the coordinates of the vertices are [latex]\left(\pm a,0\right)[/latex]
- the length of the minor axis is [latex]2b[/latex]
- the coordinates of the co-vertices are [latex]\left(0,\pm b\right)[/latex]
- the coordinates of the foci are [latex]\left(\pm c,0\right)[/latex], where [latex]{c}^{2}={a}^{2}-{b}^{2}[/latex].
The standard form of the equation of an ellipse with center [latex]\left(0,0\right)[/latex] and major axis parallel to the y-axis is
where
-
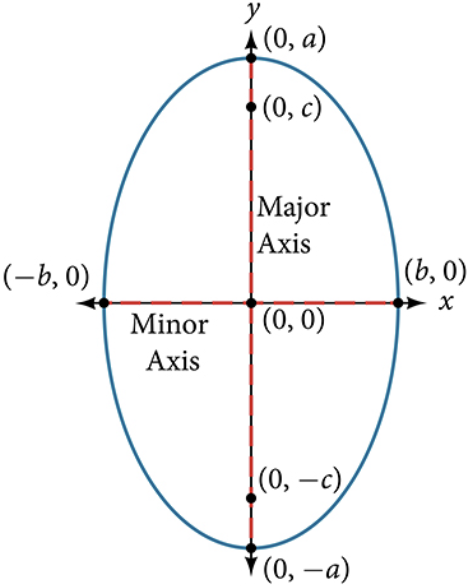
Ellipse with the y-axis as the Major Axis [latex]a>b[/latex]
- the length of the major axis is [latex]2a[/latex]
- the coordinates of the vertices are [latex]\left(0,\pm a\right)[/latex]
- the length of the minor axis is [latex]2b[/latex]
- the coordinates of the co-vertices are [latex]\left(\pm b,0\right)[/latex]
- the coordinates of the foci are [latex]\left(0,\pm c\right)[/latex], where [latex]{c}^{2}={a}^{2}-{b}^{2}[/latex].
- Determine whether the major axis is on the [latex]x[/latex]– or [latex]y[/latex]-axis.
- If the given coordinates of the vertices and foci have the form [latex](\pm a,0)[/latex] and [latex](\pm c,0)[/latex] respectively, then the major axis is parallel to the [latex]x[/latex]-axis. Use the standard form [latex]\dfrac{{x}^{2}}{{a}^{2}}+\dfrac{{y}^{2}}{{b}^{2}}=1[/latex].
- If the given coordinates of the vertices and foci have the form [latex](0,\pm a)[/latex] and [latex](0,\pm c)[/latex] respectively, then the major axis is parallel to the [latex]y[/latex]-axis. Use the standard form [latex]\dfrac{{x}^{2}}{{b}^{2}}+\dfrac{{y}^{2}}{{a}^{2}}=1[/latex].
- Use the equation [latex]c^2=a^2-b^2[/latex] along with the given coordinates of the vertices and foci, to solve for [latex]b^2[/latex].
- Substitute the values for [latex]a^2[/latex] and [latex]b^2[/latex] into the standard form of the equation determined in Step 1.
Just as we can write the equation for an ellipse given its graph, we can graph an ellipse given its equation. To graph ellipses centered at the origin, we use the standard form [latex]\dfrac{{x}^{2}}{{a}^{2}}+\dfrac{{y}^{2}}{{b}^{2}}=1,\text{ }a>b[/latex] for horizontal ellipses and [latex]\dfrac{{x}^{2}}{{b}^{2}}+\dfrac{{y}^{2}}{{a}^{2}}=1,\text{ }a>b[/latex] for vertical ellipses.
- Use the standard forms of the equations of an ellipse to determine the major axis, vertices, co-vertices, and foci.
- If the equation is in the form [latex]\dfrac{{x}^{2}}{{a}^{2}}+\dfrac{{y}^{2}}{{b}^{2}}=1[/latex], where [latex]a>b[/latex], then
- the major axis is the [latex]x[/latex]-axis
- the coordinates of the vertices are [latex]\left(\pm a,0\right)[/latex]
- the coordinates of the co-vertices are [latex]\left(0,\pm b\right)[/latex]
- the coordinates of the foci are [latex]\left(\pm c,0\right)[/latex]
- If the equation is in the form [latex]\dfrac{{x}^{2}}{{b}^{2}}+\dfrac{{y}^{2}}{{a}^{2}}=1[/latex], where [latex]a>b[/latex], then
- the major axis is the [latex]y[/latex]-axis
- the coordinates of the vertices are [latex]\left(0,\pm a\right)[/latex]
- the coordinates of the co-vertices are [latex]\left(\pm b,0\right)[/latex]
- the coordinates of the foci are [latex]\left(0,\pm c\right)[/latex]
- If the equation is in the form [latex]\dfrac{{x}^{2}}{{a}^{2}}+\dfrac{{y}^{2}}{{b}^{2}}=1[/latex], where [latex]a>b[/latex], then
- Solve for [latex]c[/latex] using the equation [latex]{c}^{2}={a}^{2}-{b}^{2}[/latex].
- Plot the center, vertices, co-vertices, and foci in the coordinate plane, and draw a smooth curve to form the ellipse.