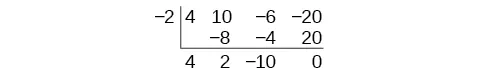Synthetic Division
As we’ve seen, long division of polynomials can involve many steps and be quite cumbersome. Synthetic division is a shorthand method of dividing polynomials for the special case of dividing by a linear factor whose leading coefficient is [latex]1[/latex].
synthetic division
Synthetic division is a shortcut that can be used when the divisor is a binomial in the form [latex]x−k[/latex] where [latex]k[/latex] is a real number. In synthetic division, only the coefficients are used in the division process.
To illustrate the process, let’s look at an example.
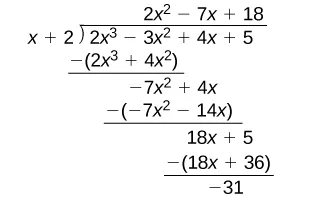
There is a lot of repetition in the table. If we don’t write the variables but, instead, line up their coefficients in columns under the division sign and also eliminate the partial products, we already have a simpler version of the entire problem.

Synthetic division carries this simplification even a few more steps. Collapse the table by moving each of the rows up to fill any vacant spots. Also, instead of dividing by [latex]2[/latex], as we would in division of whole numbers, then multiplying and subtracting the middle product, we change the sign of the “divisor” to [latex]–2[/latex], multiply and add. The process starts by bringing down the leading coefficient.
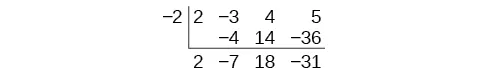
We then multiply it by the “divisor” and add, repeating this process column by column, until there are no entries left. The bottom row represents the coefficients of the quotient; the last entry of the bottom row is the remainder. In this case, the quotient is [latex]2x^2 - 7x + 18[/latex] and the remainder is [latex]-31[/latex].
- Write [latex]k[/latex] for the divisor.
- Write the coefficients of the dividend.
- Bring the lead coefficient down.
- Multiply the lead coefficient by [latex]k[/latex]. Write the product in the next column.
- Add the terms of the second column.
- Multiply the result by [latex]k[/latex]. Write the product in the next column.
- Repeat steps 5 and 6 for the remaining columns.
- Use the bottom numbers to write the quotient. The number in the last column is the remainder and has degree [latex]0[/latex], the next number from the right has degree [latex]1[/latex], the next number from the right has degree [latex]2[/latex], and so on.
Try an example on your own.