Conic Sections: Get Stronger

Circles

In the following exercises, write the standard form of the equation of the circle with the given radius and center [latex](0, 0)[/latex].

  1. Radius: [latex]7[/latex]
  2. Radius: [latex]\sqrt{2}[/latex]

In the following exercises, write the standard form of the equation of the circle with the given radius and center.

  1. Radius: [latex]1[/latex], center: [latex](3, 5)[/latex]
  2. Radius: [latex]2.5[/latex], center: [latex](1.5, -3.5)[/latex]

For the following exercises, write the standard form of the equation of the circle with the given center with point on the circle.

  1. Center [latex](3, -2)[/latex] with point [latex](3, 6)[/latex]
  2. Center [latex](4, 4)[/latex] with point [latex](2, 2)[/latex]

In the following exercises,

  1. find the center and radius
  2. graph each circle
  1. [latex](x + 5)^2 + (y + 3)^2 = 1[/latex]
  2. [latex](x - 4)^2 + (y + 2)^2 = 16[/latex]
  3. [latex]x^2 + (y + 2)^2 = 25[/latex]
  4. [latex](x - 1.5)^2 + (y + 2.5)^2 = 0.25[/latex]
  5. [latex]x^2 + y^2 = 64[/latex]
  6. [latex]2x^2 + 2y^2 = 8[/latex]

In the following exercises,

  1. identify the center and radius
  2. graph each circle
  1. [latex]x^2 + y^2 + 2x + 6y + 9 = 0[/latex]
  2. [latex]x^2 + y^2 - 4x + 10y - 7 = 0[/latex]
  3. [latex]x^2 + y^2 + 6y + 5 = 0[/latex]
  4. [latex]x^2 + y^2 + 4x = 0[/latex]

Ellipses

For the following exercises, determine whether the given equations represent ellipses. If yes, write in standard form.

  1. [latex]4x^2 + 9y^2 = 36[/latex]
  2. [latex]4x^2 + 9y^2 = 1[/latex]

For the following exercises, write the equation of an ellipse in standard form, and identify the endpoints of the major and minor axes as well as the foci.

  1. [latex]\frac{x^2}{4} + \frac{y^2}{49} = 1[/latex]
  2. [latex]x^2 + 9y^2 = 1[/latex]
  3. [latex]\frac{(x - 2)^2}{49} + \frac{(y - 4)^2}{25} = 1[/latex]
  4. [latex]\frac{(x + 5)^2}{4} + \frac{(y - 7)^2}{9} = 1[/latex]
  5. [latex]4x^2 - 8x + 9y^2 - 72y + 112 = 0[/latex]
  6. [latex]4x^2 - 24x + 36y^2 - 360y + 864 = 0[/latex]
  7. [latex]4x^2 + 40x + 25y^2 - 100y + 100 = 0[/latex]
  8. [latex]4x^2 + 24x + 25y^2 + 200y + 336 = 0[/latex]

For the following exercises, find the foci for the given ellipses.

  1. [latex]\frac{(x+3)^2}{25} + \frac{(y+1)^2}{36} = 1[/latex]
  2. [latex]x^2 + y^2 = 1[/latex]
  3. [latex]10x^2 + y^2 + 200x = 0[/latex]

For the following exercises, graph the given ellipses, noting center, vertices, and foci.

  1. [latex]\frac{x^2}{16} + \frac{y^2}{9} = 1[/latex]
  2. [latex]81x^2 + 49y^2 = 1[/latex]
  3. [latex]\frac{(x+3)^2}{9} + \frac{(y-3)^2}{9} = 1[/latex]
  4. [latex]4x^2 - 8x + 16y^2 - 32y - 44 = 0[/latex]
  5. [latex]x^2 + 8x + 4y^2 - 40y + 112 = 0[/latex]
  6. [latex]16x^2 + 64x + 4y^2 - 8y + 4 = 0[/latex]
  7. [latex]4x^2 + 16x + 4y^2 + 16y + 16 = 0[/latex]

For the following exercises, use the given information about the graph of each ellipse to determine its equation.

  1. Center at the origin, symmetric with respect to the x- and y-axes, focus at [latex](0, -2)[/latex], and point on graph [latex](5, 0)[/latex].
  2. Center [latex](4, 2)[/latex]; vertex [latex](9, 2)[/latex]; one focus: [latex](4 + 2\sqrt{6}, 2)[/latex].
  3. Center [latex](-3, 4)[/latex]; vertex [latex](1, 4)[/latex]; one focus: [latex](-3 + 2\sqrt{3}, 4)[/latex].

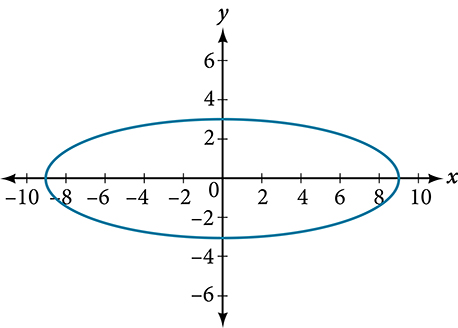
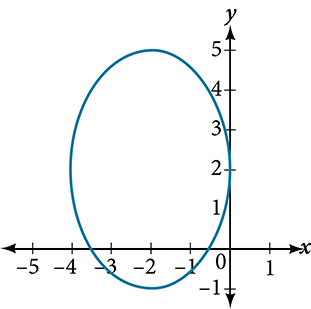
For the following exercises, given the graph of the ellipse, determine its equation.

  1. A horizontal ellipse centered at (0, 0) in the x y coordinate system with vertices at (9, 0) and (negative 9, 0) and co-vertices at (0, 3) and (0, negative 3).
  2. A vertical ellipse tangent to the y-axis at (0, 2) in the x y coordinate system and intersecting the x-axis midway between (negative 4, 0) and (negative 3, 0) and also (negative 1, 0) and (0, 0).

Real-World Applications

  1. Find the equation of the ellipse that will just fit inside a box that is four times as wide as it is high. Express in terms of [latex]h[/latex], the height.
  2. An arch has the shape of a semi-ellipse. The arch has a height of [latex]12[/latex] feet and a span of [latex]40[/latex] feet. Find an equation for the ellipse, and use that to find the distance from the center to a point at which the height is [latex]6[/latex] feet. Round to the nearest hundredth.
  3. A person in a whispering gallery standing at one focus of the ellipse can whisper and be heard by a person standing at the other focus because all the sound waves that reach the ceiling are reflected to the other person. If a whispering gallery has a length of [latex]120[/latex] feet, and the foci are located [latex]30[/latex] feet from the center, find the height of the ceiling at the center.

Hyperbolas

For the following exercises, determine whether the following equations represent hyperbolas. If so, write in standard form.

  1. [latex]\frac{x^2}{36} - \frac{y^2}{9} = 1[/latex]
  2. [latex]25x^2 - 16y^2 = 400[/latex]

For the following exercises, write the equation for the hyperbola in standard form if it is not already, and identify the vertices and foci, and write equations of asymptotes.

  1. [latex]\frac{x^2}{25} - \frac{y^2}{36} = 1[/latex]
  2. [latex]\frac{y^2}{4} - \frac{x^2}{81} = 1[/latex]
  3. [latex]\frac{(x - 1)^2}{9} - \frac{(y - 2)^2}{16} = 1[/latex]
  4. [latex]\frac{(x - 2)^2}{49} - \frac{(y + 7)^2}{49} = 1[/latex]
  5. [latex]-9x^2 - 54x + 9y^2 - 54y + 81 = 0[/latex]
  6. [latex]-4x^2 + 24x + 16y^2 - 128y + 156 = 0[/latex]
  7. [latex]x^2 + 2x - 100y^2 - 1000y + 2401 = 0[/latex]
  8. [latex]4x^2 + 24x - 25y^2+200y + 464 = 0[/latex]

For the following exercises, write the equation for the hyperbola in standard form if it is not already, and identify the vertices and foci, and write equations of asymptotes.

  1. [latex]\frac{(x - 3)^2}{5^2} - \frac{(y + 4)^2}{2^2} = 1[/latex]
  2. [latex]9x^2 - 18x - 16y^2 + 32y - 151 = 0[/latex]

For the following exercises, sketch a graph of the hyperbola, labeling vertices and foci.

  1. [latex]\frac{x^2}{49} - \frac{y^2}{16} = 1[/latex]
  2. [latex]\frac{y^2}{9} - \frac{x^2}{25} = 1[/latex]
  3. [latex]\frac{(y + 5)^2}{9} - \frac{(x - 4)^2}{25} = 1[/latex]
  4. [latex]\frac{(y - 3)^2}{9} - \frac{(x - 3)^2}{9} = 1[/latex]
  5. [latex]64x^2 + 128x - 9y^2 - 72y - 656 = 0[/latex]
  6. [latex]-100x^2 + 1000x +y^2 -10y - 2575= 0[/latex]

For the following exercises, given information about the graph of the hyperbola, find its equation.

  1. Vertices at [latex](3, 0)[/latex] and [latex](-3, 0)[/latex] and one focus at [latex](5, 0)[/latex].
  2. Vertices at [latex](1, 1)[/latex] and [latex](11, 1)[/latex] and one focus at [latex](12, 1)[/latex].
  3. Center: [latex](0, 0)[/latex]; vertex: [latex](0, -13)[/latex]; one focus: [latex]\left(0, \sqrt{313}\right)[/latex].
  4. Center: [latex](4, 2)[/latex]; vertex: [latex](9, 2)[/latex]; one focus: [latex]\left(4 + \sqrt{26}, 2\right)[/latex].

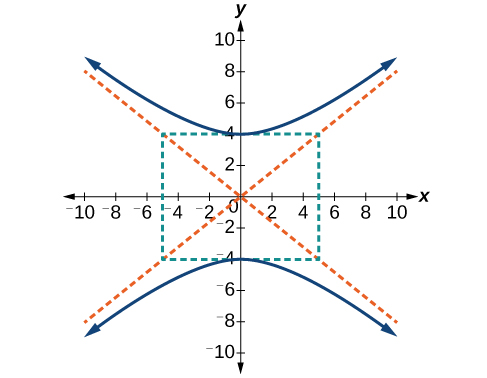
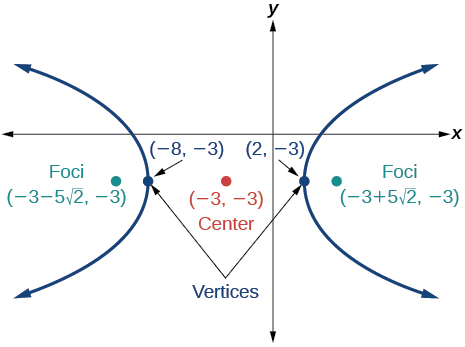
For the following exercises, given the graph of the hyperbola, find its equation.

  1. A vertical hyperbola centered at (0, 0) with vertices at (0, negative 4) and (0, 4). The slant asymptotes are shown but not labeled.
  2. A vertical hyperbola centered at (negative 1, 0) with vertices at (negative 1, negative 3) and (negative 1, 3) and foci at (negative 1, negative 3 square root of 2) and (negative 1, 3 square root of 2).
  3. A horizontal hyperbola centered at (negative 3, negative 3) with vertices at (negative 8, negative 3) and (2, negative 3) and foci at (negative 3 minus 5 square root of 2, negative 3) and (negative 3 + 5 square root of 2, negative 3).

Real-World Applications

For the following exercises, a hedge is to be constructed in the shape of a hyperbola near a fountain at the center of the yard. Find the equation of the hyperbola and sketch the graph.

  1. The hedge will follow the asymptotes [latex]y = x[/latex] and [latex]y = -x[/latex], and its closest distance to the center fountain is [latex]5[/latex] yards.
  2. The hedge will follow the asymptotes [latex]y = \frac{1}{2}x[/latex] and [latex]y = -\frac{1}{2}x[/latex], and its closest distance to the center fountain is [latex]10[/latex] yards.
  3. The hedge will follow the asymptotes [latex]y = \frac{3}{4}x[/latex] and [latex]y = -\frac{3}{4}x[/latex], and its closest distance to the center fountain is [latex]20[/latex] yards.

For the following exercises, assume an object enters our solar system and we want to graph its path on a coordinate system with the sun at the origin and the x-axis as the axis of symmetry for the object’s path. Give the equation of the flight path of each object using the given information.

  1. The object enters along a path approximated by the line [latex]y = 2x - 2[/latex] and passes within [latex]0.5[/latex] au of the sun at its closest approach, so the sun is one focus of the hyperbola. It then departs the solar system along a path approximated by the line [latex]y = -2x + 2[/latex].
  2. The object enters along a path approximated by the line [latex]y = \frac{1}{3}x - 1[/latex] and passes within [latex]1[/latex] au of the sun at its closest approach, so the sun is one focus of the hyperbola. It then departs the solar system along a path approximated by the line [latex]y = -\frac{1}{3}x + 1[/latex].

Parabolas

For the following exercises, determine whether the given equation is a parabola. If so, rewrite the equation in standard form.

  1. [latex]y = 4x^2[/latex]
  2. [latex](y - 3)^2 = 8(x - 2)[/latex]

For the following exercises, rewrite the given equation in standard form, and then determine the vertex ([latex]V[/latex]), focus ([latex]F[/latex]), and directrix ([latex]d[/latex]) of the parabola.

  1. [latex]x = 8y^2[/latex]
  2. [latex]y = -4x^2[/latex]
  3. [latex]x=36y^2[/latex]
  4. [latex](x - 1)^2 = 4(y - 1)[/latex]
  5. [latex](y - 4)^2 = 2(x + 3)[/latex]
  6. [latex](x + 4)^2 = 24(y + 1)[/latex]
  7. [latex]y^2 + 12x - 6y + 21 = 0[/latex]
  8. [latex]5x^2 - 50x - 4y + 113 = 0[/latex]
  9. [latex]x^2 - 4x + 2y - 6 = 0[/latex]
  10. [latex]3y^2 - 4x - 6y + 23 = 0[/latex]

For the following exercises, graph the parabola, labeling the focus and the directrix.

  1. [latex]x = \frac{1}{8}y^2[/latex]
  2. [latex]y = \frac{1}{36}x^2[/latex]
  3. [latex](y - 2)^2 = -\frac{4}{3}(x + 2)[/latex]
  4. [latex]-6(y + 5)^2 = 4(x - 4)[/latex]
  5. [latex]x^2 + 8x + 4y + 20 = 0[/latex]
  6. [latex]y^2 - 8x + 10y + 9 = 0[/latex]
  7. [latex]y^2 + 2y - 12x + 61 = 0[/latex]

For the following exercises, find the equation of the parabola given information about its graph.

  1. Vertex is [latex](0, 0)[/latex]; directrix is [latex]y = 4[/latex], focus is [latex](0, -4)[/latex].
  2. Vertex is [latex](2, 2)[/latex]; directrix is [latex]x = 2 - \sqrt{2}[/latex], focus is [latex](2 + \sqrt{2}, 2)[/latex].
  3. Vertex is [latex](\sqrt{2}, -\sqrt{3})[/latex]; directrix is [latex]x = 2\sqrt{2}[/latex], focus is [latex](0, -\sqrt{3})[/latex].

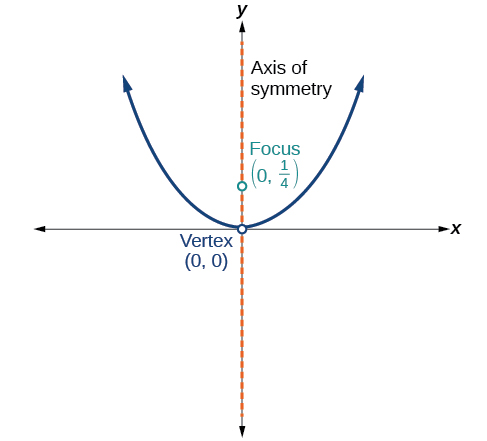
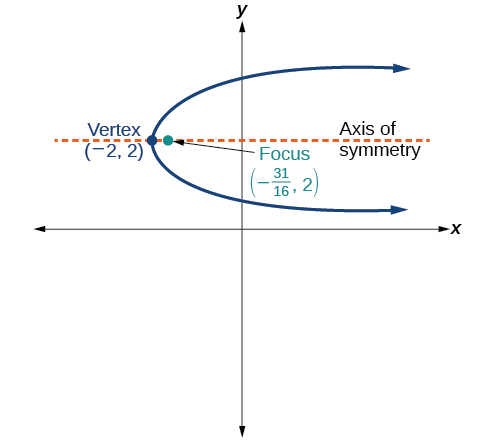
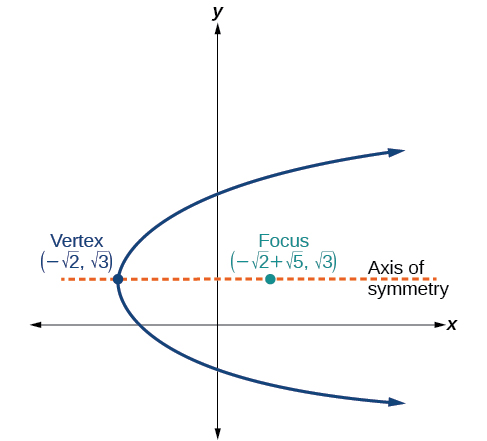
For the following exercises, determine the equation for the parabola from its graph.

  1. This figure shows two thumbtacks stuck in a piece of paper with a slack piece of string between them. A pencil pulls the string taught and by moving around, draws an ellipse.
  2. This is a horizontal parabola in the x y plane, opening to the right, with Vertex (negative 2, 2) and Focus (negative 31/16, 2). The Axis of Symmetry, a horizontal line, is shown, passing through the Vertex and the Focus.
  3. This is a horizontal parabola in the x y plane, opening to the right, with Vertex (negative square root of 2, square root of 3) and Focus (negative square root of 2 + square root of 5, square root of 3). The Axis of Symmetry, a horizontal line, is shown, passing through the Vertex and the Focus.

Real-World Applications

  1. The mirror in an automobile headlight has a parabolic cross-section with the light bulb at the focus. On a schematic, the equation of the parabola is given as [latex]x^2 = 4y[/latex]. At what coordinates should you place the light bulb?
  2. A satellite dish is shaped like a paraboloid of revolution. This means that it can be formed by rotating a parabola around its axis of symmetry. The receiver is to be located at the focus. If the dish is [latex]12[/latex] feet across at its opening and [latex]4[/latex] feet deep at its center, where should the receiver be placed?
  3. The reflector in a searchlight is shaped like a paraboloid of revolution. A light source is located [latex]1[/latex] foot from the base along the axis of symmetry. If the opening of the searchlight is [latex]3[/latex] feet across, find the depth.
  4. An arch is in the shape of a parabola. It has a span of [latex]100[/latex] feet and a maximum height of [latex]20[/latex] feet. Find the equation of the parabola, and determine the height of the arch [latex]40[/latex] feet from the center.
  5. An object is projected so as to follow a parabolic path given by [latex]y = -x^2 + 96x[/latex], where [latex]x[/latex] is the horizontal distance traveled in feet and [latex]y[/latex] is the height. Determine the maximum height the object reaches.